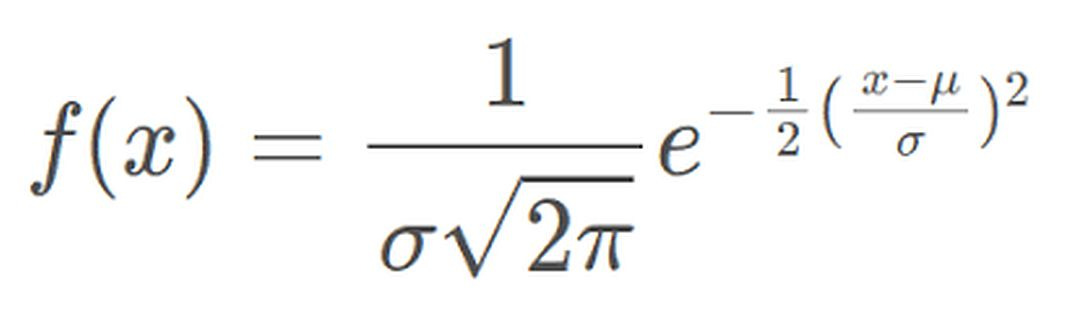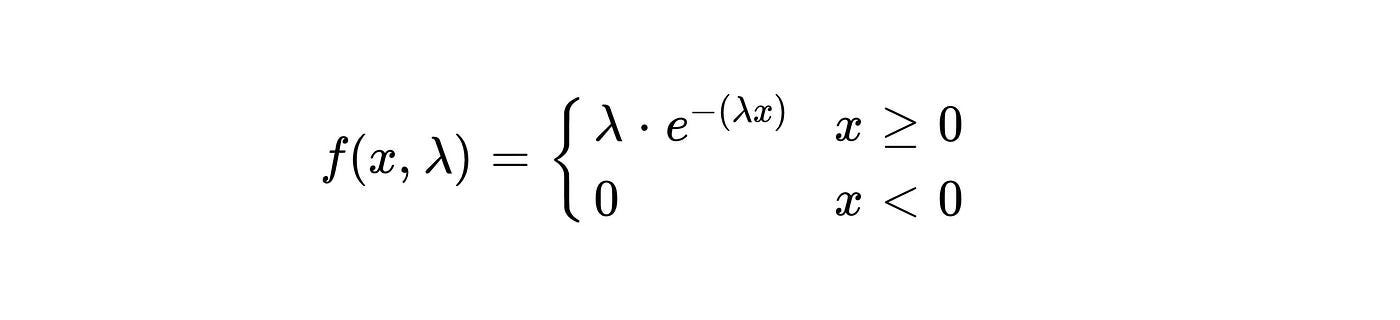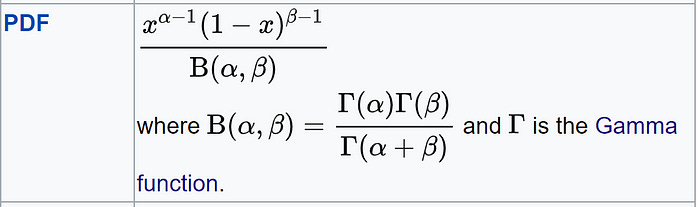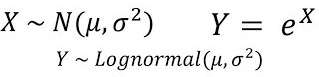11 Essential Distributions That Data Scientists Use 95% of the Time
Most important distributions in data science.
Statistical models assume an underlying data generation process.
Based on the assumed data generation process, we can:
Formulate the maximum likelihood estimation (MLE) step.
Determine the maximum likelihood estimates.
As a result, the model performance becomes entirely dependent on:
Your understanding of the data generation process.
The distribution you chose to model data with, which, in turn, depends on how well you understand various distributions.
We also looked at this in a recent deep dive on generalized linear models, where the entire performance was reliant on the data generation process we assumed: Generalized Linear Models (GLMs): The Supercharged Linear Regression.
Thus, it is crucial to be aware of some of the most important distributions and the type of data they can model.
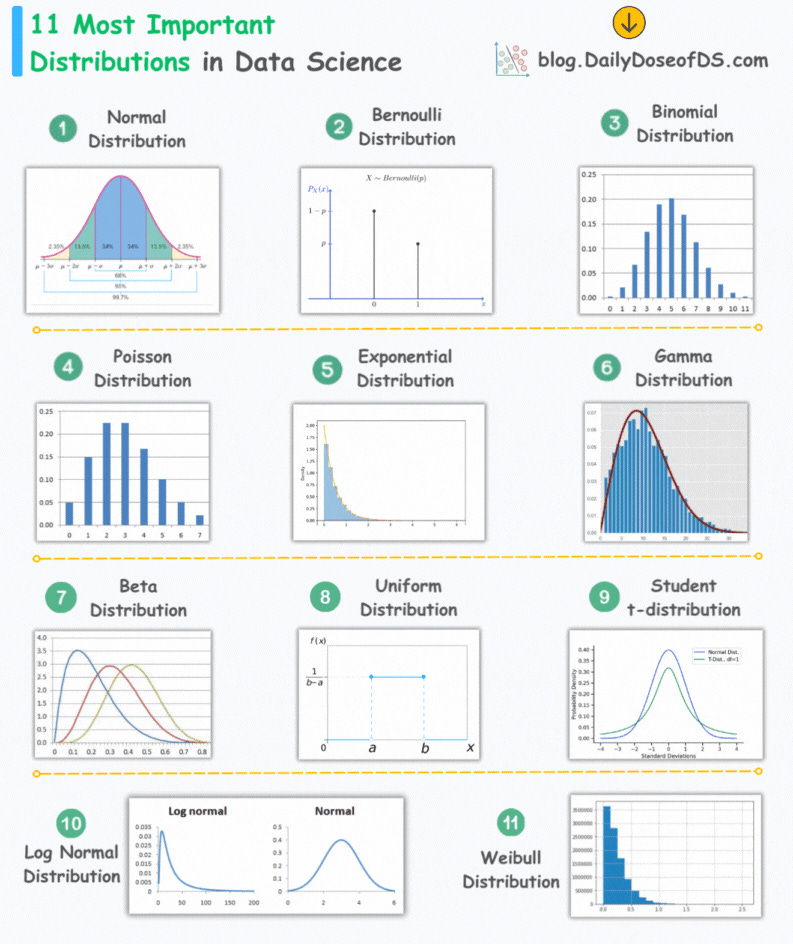
The visual below depicts the 11 most important distributions in data science:
Today, let’s understand them briefly and how they are used.
Normal Distribution
Normal distribution PDF The most widely used distribution in data science.
Characterized by a symmetric bell-shaped curve
It is parameterized by two parameters—mean and standard deviation.
Example: Height of individuals.
Bernoulli Distribution
Bernouilli PDF A discrete probability distribution that models the outcome of a binary event.
It is parameterized by one parameter—the probability of success.
Example: Modeling the outcome of a single coin flip.
Binomial Distribution
Binomial Distribution PDF It is Bernoulli distribution repeated multiple times.
A discrete probability distribution that represents the number of successes in a fixed number of independent Bernoulli trials.
It is parameterized by two parameters—the number of trials and the probability of success.
Poisson Distribution
Poisson Distribution PDF A discrete probability distribution that models the number of events occurring in a fixed interval of time or space.
It is parameterized by one parameter—lambda, the rate of occurrence.
Example: Analyzing the number of goals a team will score during a specific time period.
Exponential Distribution
Exponential Distribution PDF A continuous probability distribution that models the time between events occurring in a Poisson process.
It is parameterized by one parameter—lambda, the average rate of events.
Example: Analyzing the time between goals scored by a team.
Gamma Distribution
Gamma Distribution PDF It is a variation of the exponential distribution.
A continuous probability distribution that models the waiting time for a specified number of events in a Poisson process.
It is parameterized by two parameters—alpha (shape) and beta (rate).
Example: Analysing the time it would take for a team to score, say, three goals.
Beta Distribution
Beta Distribution PDF It is used to model probabilities, thus, it is bounded between [0,1].
Differs from Binomial in this respect that in Binomial, probability is a parameter.
But in Beta, the probability is a random variable.
Uniform Distribution
Uniform Distribution PDF All outcomes within a given range are equally likely.
It can be continuous or discrete.
It is parameterized by two parameters: a (minimum value) and b (maximum value).
Example: Simulating the roll of a fair six-sided die, where each outcome (1, 2, 3, 4, 5, 6) has an equal probability.
Log-Normal Distribution
Log-Normal Distribution PDF A continuous probability distribution where the logarithm of the variable follows a normal distribution.
It is parameterized by two parameters—mean and standard deviation.
Example: Typically, in stock returns, the natural logarithm follows a normal distribution.
Student t-distribution
It is similar to normal distribution but with longer tails.
It is used in t-SNE to model low-dimensional pairwise similarities. We covered it here: t-SNE article.
Weibull
Models the waiting time for an event.
Often employed to analyze time-to-failure data.
👉 Over to you: Which important distributions have I missed here?
👉 If you liked this post, don’t forget to leave a like ❤️. It helps more people discover this newsletter on Substack and tells me that you appreciate reading these daily insights. The button is located towards the bottom of this email.
Thanks for reading!
Latest full articles
If you’re not a full subscriber, here’s what you missed last month:
Why Bagging is So Ridiculously Effective At Variance Reduction?
Sklearn Models are Not Deployment Friendly! Supercharge Them With Tensor Computations.
Deploy, Version Control, and Manage ML Models Right From Your Jupyter Notebook with Modelbit
Model Compression: A Critical Step Towards Efficient Machine Learning.
Gaussian Mixture Models (GMMs): The Flexible Twin of KMeans.
To receive all full articles and support the Daily Dose of Data Science, consider subscribing:
👉 Tell the world what makes this newsletter special for you by leaving a review here :)
👉 If you love reading this newsletter, feel free to share it with friends!
Isn’t the binomial distribution just a special case of the Bernoulli distribution?