25 Most Important Mathematical Definitions in DS

Apr 11, 2025

Visual question answering, image captioning, and multimodal content generation in your own VPC. 100% secure and private, and requires just two steps:

Thanks to LightningAI for partnering today!

Here’s a visual with some of the most important mathematical formulations used in Data Science and Statistics (in no specific order).

Before reading ahead, look at them one by one and calculate how many of them do you already know:

Some of the terms are pretty self-explanatory, so we won’t go through each of them, like:

Gradient Descent, Normal Distribution, Sigmoid, Correlation, Cosine similarity, Naive Bayes, F1 score, ReLU, Softmax, MSE, MSE + L2 regularization, KMeans, Linear regression, SVM, Log loss.

Here are the remaining terms:

MLE (Maximum Likelihood Estimation): A method for estimating the parameters of a statistical model by maximizing the likelihood of the observed data.
Z-score: A standardized value that indicates how many standard deviations a data point is from the mean.
Ordinary Least Squares: A closed-form solution for linear regression obtained using the MLE step mentioned above.
Entropy: A measure of the uncertainty or randomness of a random variable. It is often utilized in decision trees and the t-SNE algorithm.
Eigen Vectors: The non-zero vectors that do not change their direction when a linear transformation is applied. It is widely used in dimensionality reduction techniques like PCA. Here’s how.
R2 (R-squared): A statistical measure that represents the proportion of variance explained by a regression model:

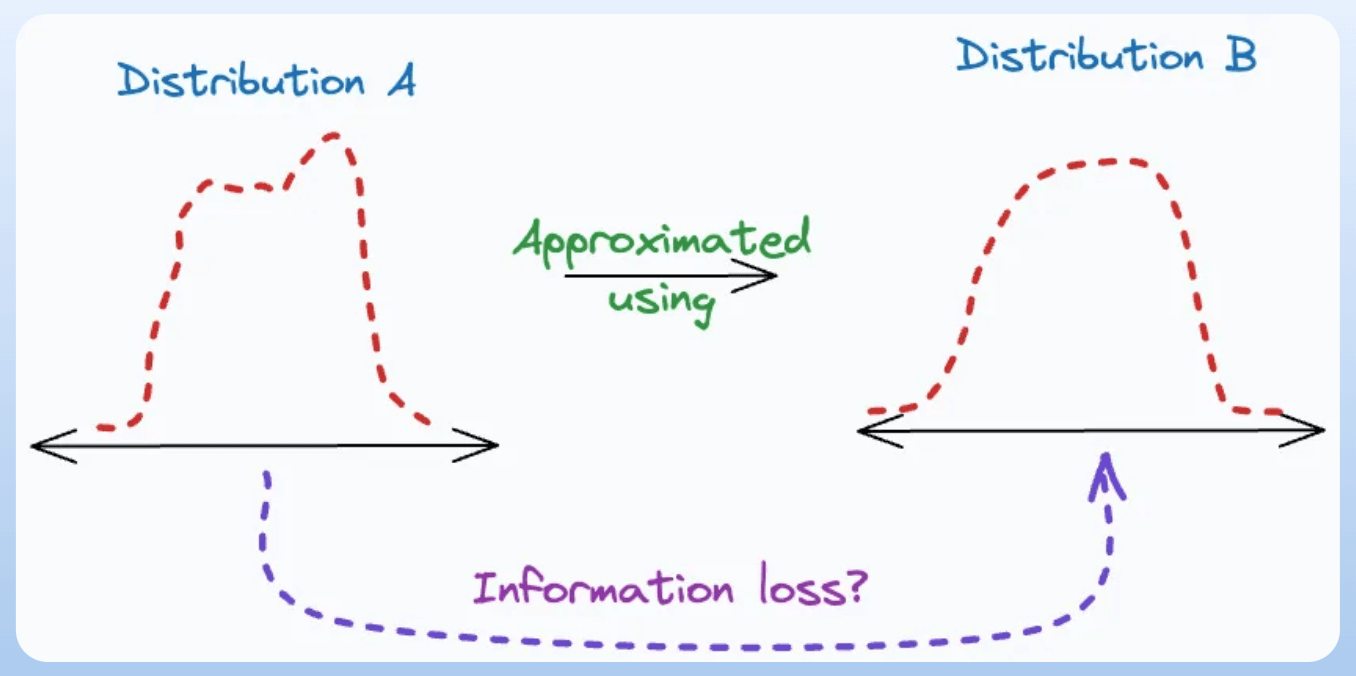
KL divergence: Assess how much information is lost when one distribution is used to approximate another distribution. It is used as a loss function in the t-SNE algorithm. We discussed it here: t-SNE article.

SVD: A factorization technique that decomposes a matrix into three other matrices, often noted as U, Σ, and V. It is fundamental in linear algebra for applications like dimensionality reduction, noise reduction, and data compression.
Lagrange multipliers: They are commonly used mathematical techniques to solve constrained optimization problems.
- For instance, consider an optimization problem with an objective function f(x) and assume that the constraints are g(x)=0 and h(x)=0. Lagrange multipliers help us solve this.
- We covered them in detail here.

How many terms did you know? Let me know.

👉 Over to you: Of course, this is not an all-encompassing list. What other mathematical definitions will you include here?

Thanks for reading!

At the end of the day, all businesses care about impact. That’s it!

We have discussed several other topics (with implementations) that align with such topics.

Here are some of them:

Learn how to build Agentic systems in an ongoing crash course with 6 parts.
Learn how to build real-world RAG apps and evaluate and scale them in this crash course.

Learn sophisticated graph architectures and how to train them on graph data in this crash course.
So many real-world NLP systems rely on pairwise context scoring. Learn scalable approaches here.
Learn how to run large models on small devices using Quantization techniques.
Learn how to generate prediction intervals or sets with strong statistical guarantees for increasing trust using Conformal Predictions.
Learn how to identify causal relationships and answer business questions using causal inference in this crash course.
Learn how to scale and implement ML model training in this practical guide.
Learn techniques to reliably test new models in production.
Learn how to build privacy-first ML systems using Federated Learning.
Learn 6 techniques with implementation to compress ML models.

All these resources will help you cultivate key skills that businesses and companies care about the most.

Daily Dose of Data Science