A Common Misconception About Boosting

Boosting != Tree-based boosting.

Daily Dose of Data Science Free Book | Deep Dives

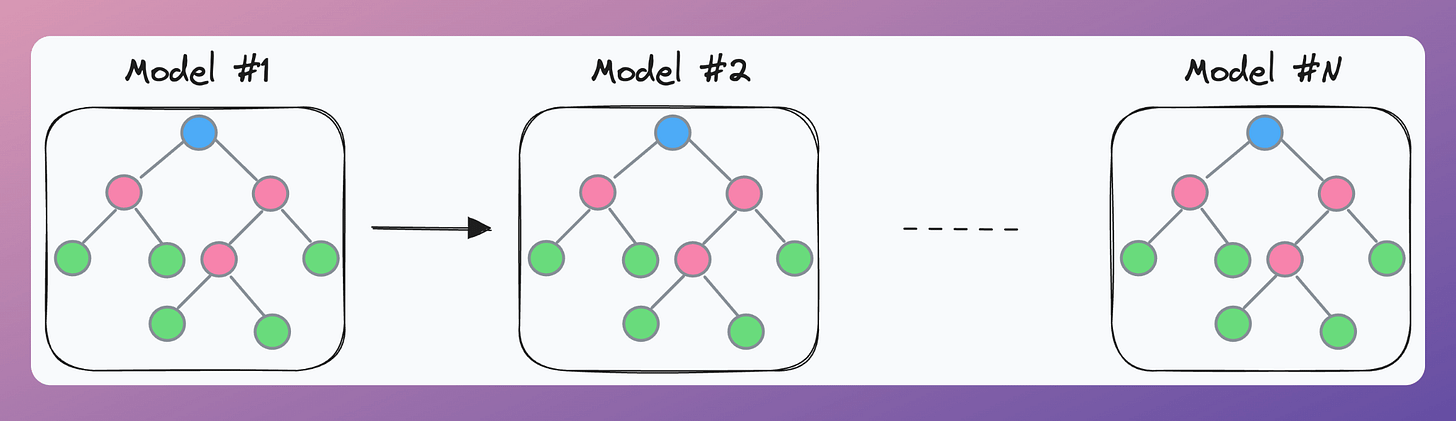
Usually, whenever we hear about Boosting, we tend to associate the idea with a combination of tree-based models:

Of course, there’s nothing wrong since trees, particularly decision stumps (trees with a single split), are the most common base learners with boosting algorithms like AdaBoost.

But this DOES NOT mean that AdaBoost can only work with trees.

This is something I have noticed in several texts written about boosting. More specifically, they start with the idea of utilizing “weak learners” but then immediately pivot to trees.

Why do they do that, and what are we missing here?

Let’s dive in!

---

Background

To understand why AdaBoost is a broader concept that does not necessarily have to be associated with trees, we need to know how it works.

Let’s consider a straightforward implementation of Boosting, which we've covered in this newsletter before.

The idea is simple:

Boosting = The subsequent model must utilize information from the previous model to form a more informed model.

Consider the following dummy dataset:

We construct the first tree on this dataset as follows:

Measuring the performance (R2), we get:

Now, we must construct the next tree. To do this, we fit another model on the residuals (true-predicted) of the first tree:

Yet again, we measure the performance of the current ensemble:

Tree1 captures some variance, and tree2 captures the residual left by tree1. So the final prediction is the sum of both predictions.

The R2 score has jumped from 0.68 to 0.81.

Now, let’s construct another tree on the residuals (true-predicted) of the current ensemble:

Let’s measure the performance once again:

The R2 score has jumped from 0.81 to ~0.88.

We can continue to build the ensemble this way and generate better scores.

---

Take a moment to reflect on what we just did in the above implementation:

• We trained a decision tree model.

• We calculated the left-over residual.

• We trained the next model on this left-over residual.

Now, if you look at it closely, was it really necessary to use a tree there?

No, right?

All we needed was the residual term, which, of course, could have come from ANY REGRESSION MODEL:

• Can we use linear regression? → It wouldn’t be a good choice, but technically, yes, we can do that.

• Can we use a support vector regressor? → SVMs are generally strong learners, but again, technically, we can do that.

So, to summarize, while AdaBoost is often associated with trees, the algorithm itself is agnostic to the type of base learner used.

If you use sklearn, it is actually possible to employ a different base learner with AdaBoost, as shown in the implementation for a classification use case below:

---

So why trees?

While I couldn’t find a decent supporting answer for this during my research, let me share why I think we typically only build tree-based boosting models.

To begin, tabular data is quite complex:

• Variables can be skewed.

• Features can have missing values.

• Different features can have different scales.

• There can be categorical variables.

• And more.

Using standard algorithms as base learners will require extensive data cleaning and feature engineering.

But this isn’t the case with tree-based models. You can just plug them into any dataset and overfit, as demonstrated in the code below:

Attempting to fit the residuals with linear regression, for instance, would demand some engineering effort:

Since we are continuously adding a new model to fit the left-over residual, the distribution of the dependent variable (residual in case of regression) is also evolving.

The feature engineering applied during the first step of boosting will likely not be helpful in the subsequent steps and may require further manual interference.

Using tree models, however, resolves this due to their ability to operate on any kind of data.

While boosting models typically prefer tree-based learners for their robustness and adaptability, it's important to remember that you’re not bound to this choice. There’s no strict rule preventing the use of other low-bias, high-variance learners, such as mini versions of neural networks.

Hope you learned something new today!

Further reading:

• Here, we formulated the entire XGBoost algorithm from scratch, covering the mathematical foundations, and then implemented it in NumPy.

👉 Over to you: Why do you think we typically prefer tree models as base learners in boosting?

---

Every week, I publish no-fluff deep dives on topics that truly matter to your skills for ML/DS roles.

For instance:

• A Crash Course on Graph Neural Networks (Implementation Included)

• Formulating and Implementing XGBoost From Scratch

• A Crash Course of Model Calibration – Part 1

• A Crash Course of Model Calibration – Part 2

• Conformal Predictions: Build Confidence in Your ML Model’s Predictions

• Quantization: Optimize ML Models to Run Them on Tiny Hardware

• A Crash Course on Causality – Part 1

• A Crash Course on Causality – Part 2

• 5 Must-Know Ways to Test ML Models in Production (Implementation Included)

• A Beginner-Friendly Guide to Multi-GPU Model Training

• And many many more.

Join below to unlock all full articles:

---

SPONSOR US

Get your product in front of 85,000 data scientists and other tech professionals.

Our newsletter puts your products and services directly in front of an audience that matters — thousands of leaders, senior data scientists, machine learning engineers, data analysts, etc., who have influence over significant tech decisions and big purchases.

To ensure your product reaches this influential audience, reserve your space here or reply to this email to ensure your product reaches this influential audience.