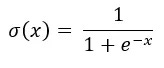A Highly Overlooked Point In The Implementation of Sigmoid Function
Some subtle stuff that is often ignored.
There are two variations of the sigmoid function:
Standard: with an exponential term
e^(-x)in the denominator only.
Rearranged: with an exponential term
e^xin both numerator and denominator.
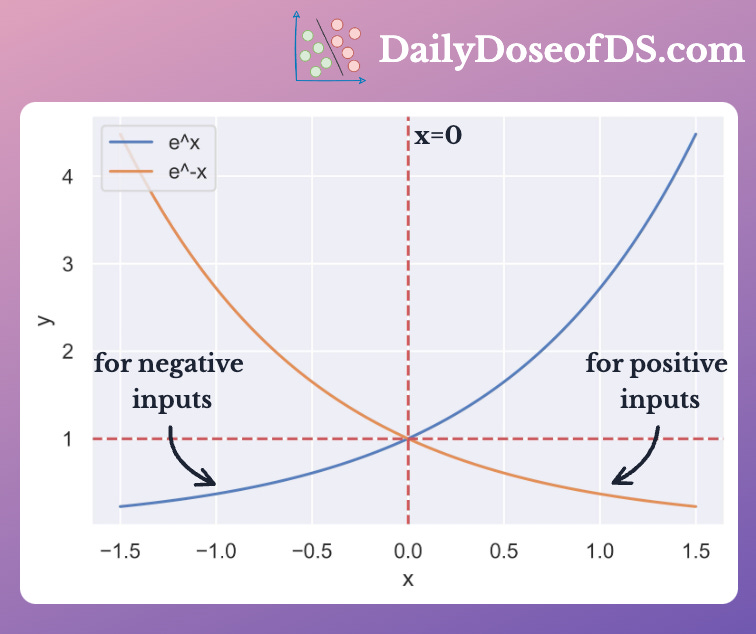
The standard sigmoid function can be easily computed for positive values. However, for large negative values, it raises overflow errors.
This is because, for large negative inputs, e^(-x) gets bigger and bigger.
To avoid this, use both variations of sigmoid.
Standard variation for positive inputs. This prevents overflow that may occur for negative inputs.
Rearranged variation for negative inputs. This prevents overflow that may occur for positive inputs.
This way, you can maintain numerical stability by preventing overflow errors in your ML pipeline.
Having said that, luckily, if you are using an existing framework, like Pytorch, you don’t need to worry about this.
These implementations offer numerical stability by default. However, if you have a custom implementation, do give it a thought.
Over to you:
Sigmoids’s two-variation implementation that I have shared above isn’t vectorized. What is your solution to vectorize this?
What are some other ways in which numerical instability may arise in an ML pipeline? How to handle them?
👉 Read what others are saying about this post on LinkedIn and Twitter.
👉 Tell the world what makes this newsletter special for you by leaving a review here :)
👉 If you liked this post, don’t forget to leave a like ❤️. It helps more people discover this newsletter on Substack and tells me that you appreciate reading these daily insights. The button is located towards the bottom of this email.
👉 If you love reading this newsletter, feel free to share it with friends!
Find the code for my tips here: GitHub.
I like to explore, experiment and write about data science concepts and tools. You can read my articles on Medium. Also, you can connect with me on LinkedIn and Twitter.