A Lesser-known Advantage of Using L2 Regularization
An untaught advantage of L2 regularization that most data scientists don't know.
Almost every tutorial/course/blog mentioning L2 regularization I have seen talks about just one thing:
L2 regularization is a machine learning technique that avoids overfitting by introducing a penalty term into the model’s loss function based on the squares of the model’s parameters.
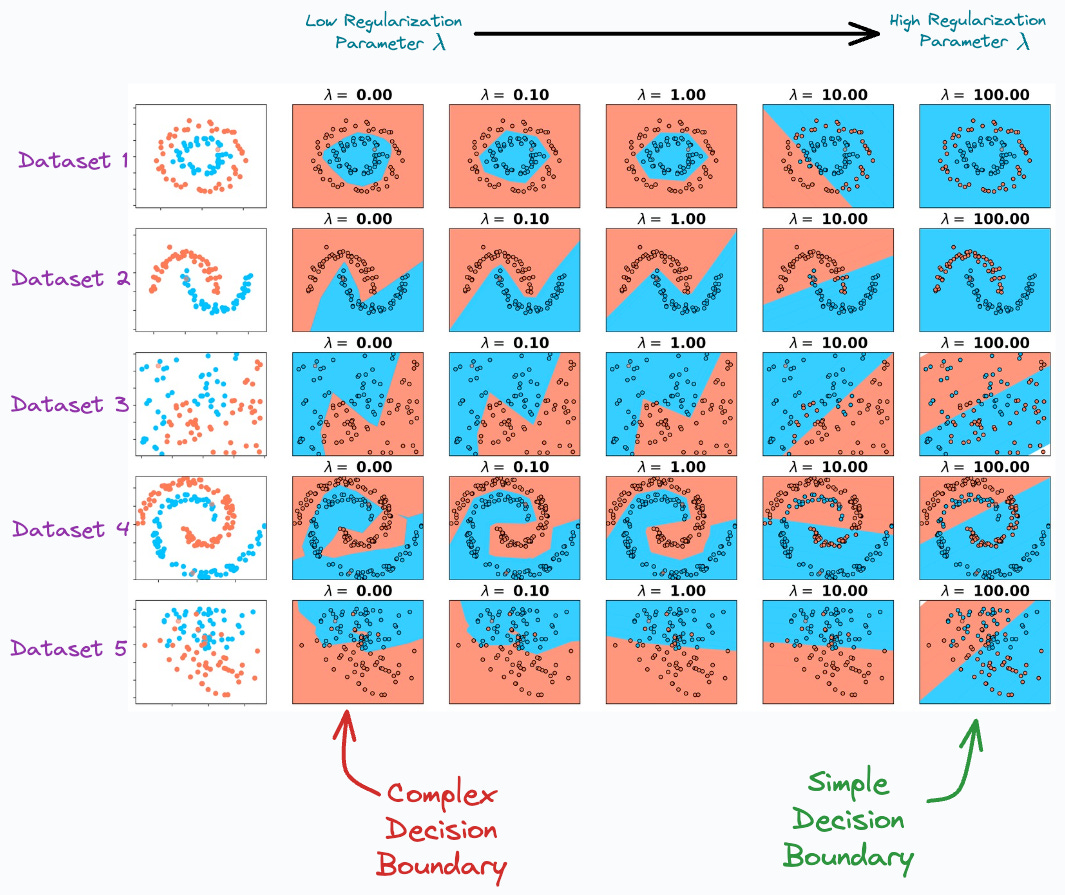
In classification tasks, for instance, increasing the effect of regularization will produce simpler decision boundaries.
Of course, the above statements are indeed correct, and I am not denying that.
In fact, we can also verify this from the diagram below:
In the image above, as we move to the right, the regularization parameter increases, and the model creates a simpler decision boundary on all 5 datasets.
Note: If you want to learn about the probabilistic origin of L2 regularization, check out this article: The Probabilistic Origin of Regularization.
Coming back to the topic…
However, what disappoints me the most is that most resources don’t point out that L2 regularization is a great remedy for multicollinearity.
Multicollinearity arises when two (or more) features are highly correlated OR two (or more) features can predict another feature:
When we use L2 regularization in linear regression, the algorithm is also called Ridge regression.
But how does L2 regularization eliminate multicollinearity?
Today, let me provide you a demonstrative intuition into this topic, which will also explain why “ridge regression” is called “ridge regression.”
Let’s begin!
Dummy dataset
For demonstration purposes, consider this dummy dataset of two features:
As shown above, we have intentionally made featureB highly correlated with featureA. This gives us a dummy dataset to work with.
Going ahead, we shall be ignoring any intercept term for simplicity.
Linear regression without L2 penalty
During regression modeling, the goal is to determine those specific parameters (θ₁, θ₂), which minimizes the residual sum of squares (RSS):
So how about we do the following:
We shall plot the RSS value for many different combinations of (θ₁, θ₂) parameters. This will create a 3D plot:
x-axis → θ₁
y-axis → θ₂
z-axis → RSS value
Next, we shall visually assess this plot to locate those specific parameters (θ₁, θ₂) that minimize the RSS value.
Let’s do this.
Without the L2 penalty, we get the following plot (it’s the same plot but viewed from different angles):
Did you notice something?
The 3D plot has a valley. There are multiple combinations of parameter values (θ₁, θ₂) for which RSS is minimum.
Thus, obtaining a single value for the parameters (θ₁, θ₂) that minimize the RSS is impossible.
Linear regression with L2 penalty
When using an L2 penalty, the goal is to minimize the following:
Creating the same plot again as we did above, we get the following:
Did you notice something different this time?
As depicted above, using L2 regularization removes the valley we saw earlier and provides a global minima to the RSS error.
Now, obtaining a single value for the parameters (θ₁, θ₂) that minimizes the RSS is possible.
Out of nowhere, L2 regularization helped us eliminate multicollinearity.
Why the name “ridge regression”?
In fact, this is where “ridge regression” also gets its name from — it eliminates the ridge in the likelihood function when the L2 penalty is used.
Of course, in the demonstrations we discussed earlier, we noticed a valley, not a ridge.
However, in that case, we were considering the residual sum of error — something which is minimized to obtain the optimal parameters.
Thus, the error function will obviously result in a valley.
If we were to use likelihood instead — something which is maximized, it would (somewhat) invert the graph upside down and result in a ridge instead:
Apparently, while naming the algorithm, the likelihood function was considered.
And that is why it was named “ridge regression.”
Pretty cool, right?
When I first learned about this some years back, I literally had no idea that such deep thought went into naming ridge regression.
Hope you learned something new today :)
If you want to learn about the probabilistic origin of L2 regularization, check out this article: The Probabilistic Origin of Regularization.
While most of the community appreciates the importance of regularization, in my experience, very few learn about its origin and the mathematical formulation behind it.
It can’t just appear out of nowhere, can it?
Also, if you love to dive into the mathematical details, here are some topics that would interest you:
You Are Probably Building Inconsistent Classification Models Without Even Realizing
Why Sklearn’s Logistic Regression Has no Learning Rate Hyperparameter?
👉 Over to you: What are some other advantages of using L2 regularization?
For those who want to build a career in DS/ML on core expertise, not fleeting trends:
Every week, I publish no-fluff deep dives on topics that truly matter to your skills for ML/DS roles.
For instance:
Conformal Predictions: Build Confidence in Your ML Model’s Predictions
Quantization: Optimize ML Models to Run Them on Tiny Hardware
5 Must-Know Ways to Test ML Models in Production (Implementation Included)
Implementing Parallelized CUDA Programs From Scratch Using CUDA Programming
And many many more.
Join below to unlock all full articles:
SPONSOR US
Get your product in front of ~90,000 data scientists and other tech professionals.
Our newsletter puts your products and services directly in front of an audience that matters — thousands of leaders, senior data scientists, machine learning engineers, data analysts, etc., who have influence over significant tech decisions and big purchases.
To ensure your product reaches this influential audience, reserve your space here or reply to this email to ensure your product reaches this influential audience.












The article explains that linear regression always has infinitely solutions. In reality, having more than one solution is very uncommon, almost artificial, although possible in some practical cases. Regularization can help avoid this problem, but it too can result in more than one solution in very exceptional cases.
Wow I follow the articles weekly , today's one was great , got to know a lot of things. Can you write the code for generating the 3D plots.