A Lesser-Known Detail of Dropout

Here's the remaining information which you must know.

Avi Chawla

Oct 06, 2024

Daily Dose of Data Science Free Book | Deep Dives

Here’s what most resources/tutorials mention about Dropout:

Zero out neurons randomly in a neural network. This is done to regularize the network.

Dropout is only applied during training, and which neuron activations to zero out (or drop) is decided using a Bernoulli distribution:

“`p`” is the dropout probability specified in, say, PyTorch → `nn.Dropout(p)`.

Of course, these details are correct.

But this is just 50% of how Dropout works.

If you are only aware of the 50% details I mentioned above, then continue reading as there’s new information for you.

How Dropout actually works?

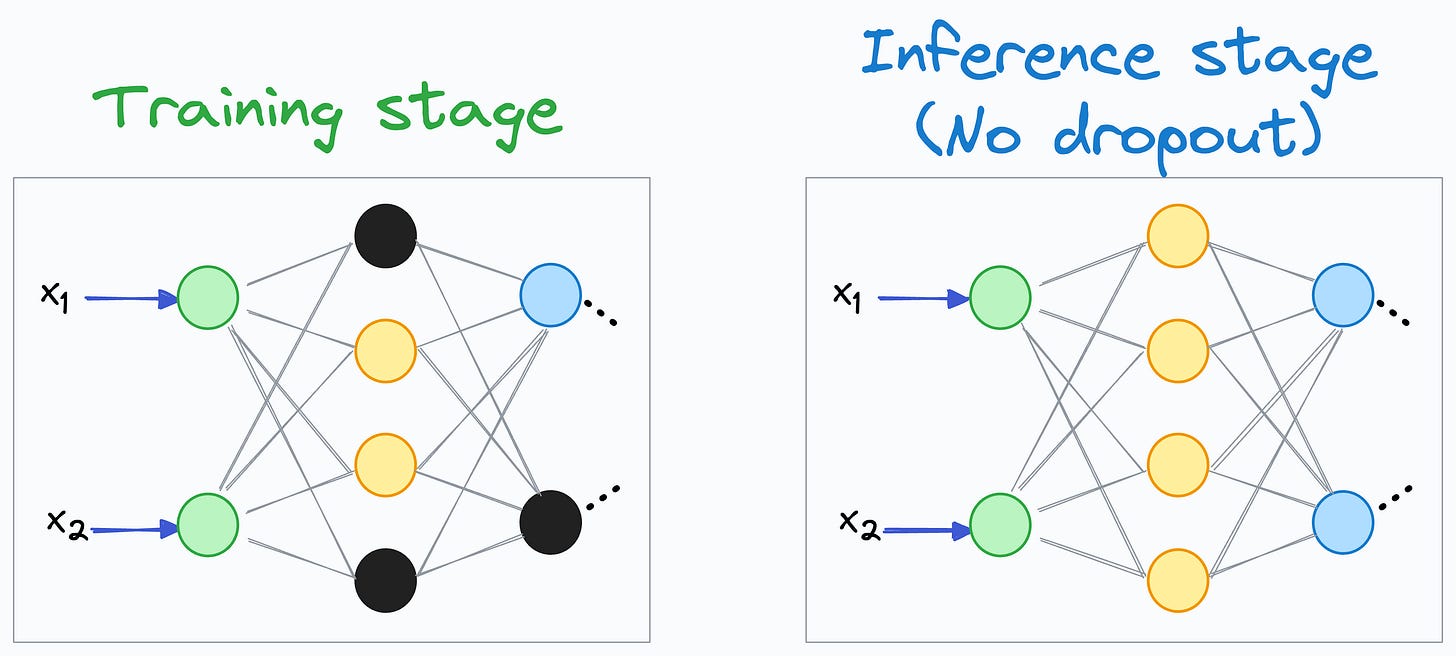
To begin, we must note that Dropout is only applied during training, but not during the inference/evaluation stage:

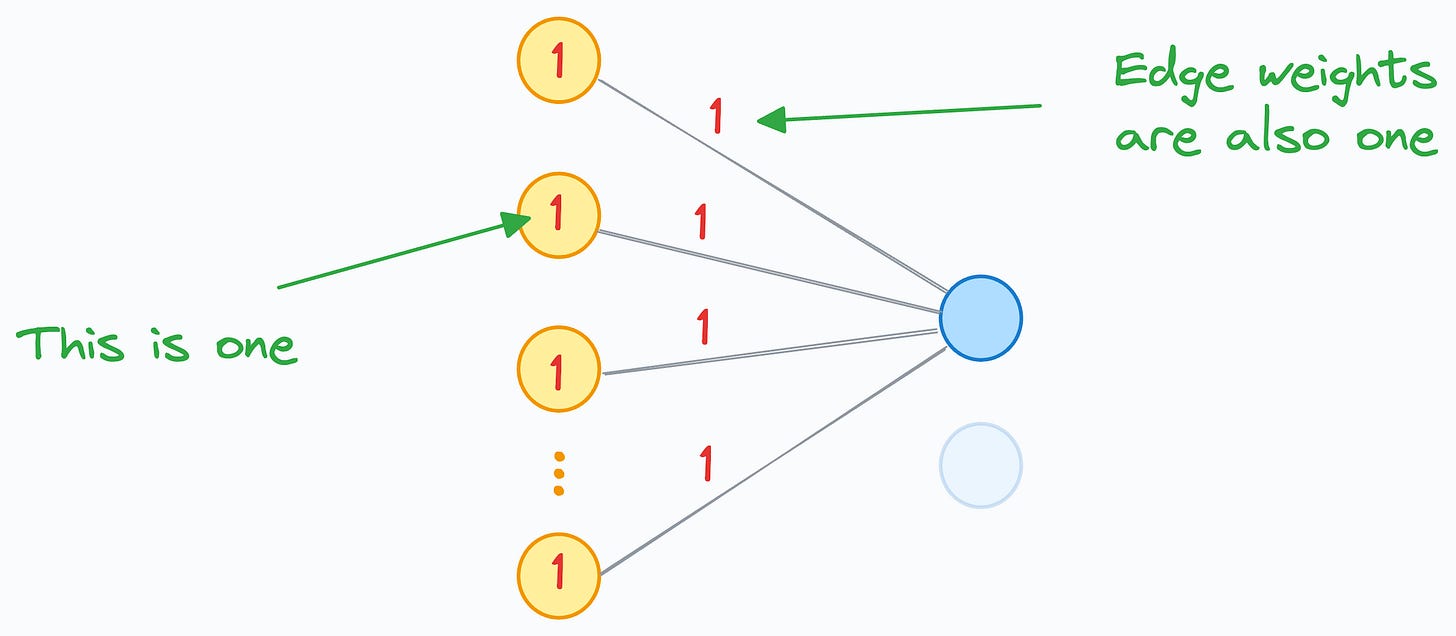
Now, consider that a neuron’s input is computed using 100 neurons in the previous hidden layer:

For simplicity, let’s assume a couple of things here:

The activation of every yellow neuron is 1.
The edge weight from the yellow neurons to the blue neuron is also 1.

As a result, the input received by the blue neuron will be 100, as depicted below:

All good?

Now, during training, if we were using Dropout with, say, a 40% dropout rate, then roughly 40% of the yellow neuron activations would have been zeroed out.

As a result, the input received by the blue neuron would have been around 60, as depicted below:

However, the above point is only valid for the training stage.

If the same scenario had existed during the inference stage instead, then the input received by the blue neuron would have been 100.

Thus, under similar conditions:

The input received during training → 60.
The input received during inference → 100.

Do you see any problem here?

During training, the average neuron inputs are significantly lower than those received during inference.

More formally, using Dropout significantly affects the scale of the activations.

However, it is desired that the neurons throughout the model must receive the roughly same mean (or expected value) of activations during training and inference.

To address this, Dropout performs one additional step.

This idea is to scale the remaining active inputs during training.

The simplest way to do this is by scaling all activations during training by a factor of 1/(1-p), where p is the dropout rate.

For instance, using this technique on the neuron input of 60, we get the following (recall that we set p=40%):

As depicted above, scaling the neuron input brings it to the desired range, which makes training and inference stages coherent for the network.

Verifying experimentally

In fact, we can verify that typical implementations of Dropout, from PyTorch, for instance, do carry out this step.

Let’s define a dropout layer as follows:

Now, let’s consider a random tensor and apply this dropout layer to it:

As depicted above, the retained values have increased.

The second value goes from 0.13 → 0.16.
The third value goes from 0.93 → 1.16.
and so on…

What’s more, the retained values are precisely the same as we would have obtained by explicitly scaling the input tensor with 1/(1-p):

If we were to do the same thing in evaluation mode instead, we notice that no value is dropped and no scaling takes place either, which makes sense as Dropout is only used during training:

This is the remaining 50% details, which, in my experience, most resources do not cover, and as a result, most people aren’t aware of.

But it is a highly important step in Dropout since it maintains numerical coherence between training and inference stages.

With that, now you know 100% of how Dropout works.

Here are some more missing details that I don’t see people talk about often:

Why Sklearn’s Logistic Regression Has No Learning Rate Hyperparameter?
- Gradient descent is a typical way to train logistic regression.
- But if that is the case, then why there’s no learning rate hyperparameter (α) in its sklearn implementation:
- Moreover, the parameter list has the ‘max_iter’ parameter that intuitively looks analogous to the epochs.
- We have epochs but no learning rate (α), so how do we even update the model parameters using SGD?
- Learn this here: Why Sklearn’s Logistic Regression Has No Learning Rate Hyperparameter?
Why Bagging is So Ridiculously Effective At Variance Reduction?
- Everyone says we must sample rows from the training dataset with replacement. Why?
- Also, how to mathematically formulate the idea of Bagging and prove variance reduction.
- Read this to learn more: Why Bagging is So Ridiculously Effective At Variance Reduction?