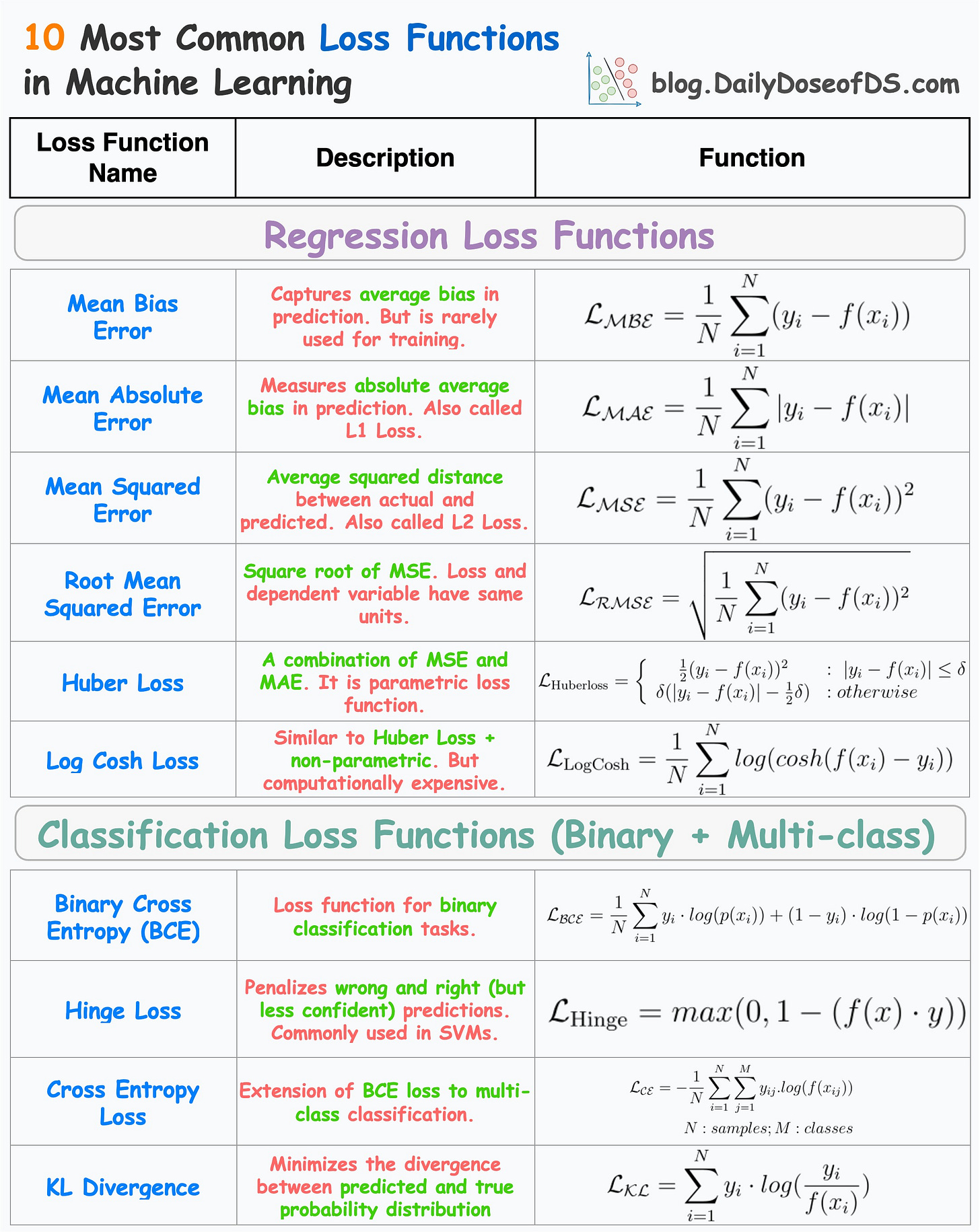
A Single Frame Summary of 10 Most Common Regression and Classification Loss Functions
10 must know loss functions, along with their limitations and benefits.
Loss functions are a key component of ML algorithms.
They specify the objective an algorithm should aim to optimize during its training. In other words, loss functions tell the algorithm what it should minimize or maximize to improve its performance.
Therefore, being aware of the most common loss functions is extremely crucial.
The visual below depicts the most commonly used loss functions for regression and classification tasks.
Regression
Mean Bias Error
Captures the average bias in the prediction.
However, it is rarely used in training ML models.
This is because negative errors may cancel positive errors, leading to zero loss, and consequently, no weight updates.
Mean bias error is foundational to the more advanced regression losses discussed below.
Mean Absolute Error (or L1 loss)
Measures the average absolute difference between predicted and actual value.
Positive errors and negative errors don’t cancel out.
One caveat is that small errors are as important as big ones. Thus, the magnitude of the gradient is independent of error size.
Mean Squared Error (or L2 loss)
It measures the squared difference between predicted and actual value.
Larger errors contribute more significantly than smaller errors.
The above point may also be a caveat as it is sensitive to outliers.
Yet, it is among the most common loss functions for many regression models. If you want to understand the origin of mean squared error, we discussed it in this newsletter issue: Why Mean Squared Error (MSE)?
Root Mean Squared Error
Mean Squared Error with a square root.
Loss and the dependent variable (y) have the same units.
Huber Loss
It is a combination of mean absolute error and mean squared error.
For smaller errors, mean squared error is used, which is differentiable through (unlike MAE, which is non-differentiable at
x=0).For large errors, mean absolute error is used, which is less sensitive to outliers.
One caveat is that it is parameterized — adding another hyperparameter to the list.
Read this full issue to learn more about Huber Regression: A Simple Technique to Robustify Linear Regression to Outliers
Log Cosh Loss
For small errors, log cash loss is approximately →
x²/2— quadratic.For large errors, log cash loss is approximately →
|x| - log(2)— linear.Thus, it is very similar to Huber loss.
Also, it is non-parametric.
The only caveat is that it is a bit computationally expensive.
Classification
Binary cross entropy (BCE) or Log loss
A loss function used for binary classification tasks.
Measures the dissimilarity between predicted probabilities and true binary labels, through the logarithmic loss.
Where did the log loss originate from? We discussed it here: why Do We Use log-loss To Train Logistic Regression?
Hinge Loss
Penalizes both wrong and right (but less confident) predictions).
It is based on the concept of margin, which represents the distance between a data point and the decision boundary.
The larger the margin, the more confident the classifier is about its prediction.
Particularly used to train support vector machines (SVMs).
Cross-Entropy Loss
An extension of Binary Cross Entropy loss to multi-class classification tasks.
KL Divergence
Measure information lost when one distribution is approximated using another distribution.
The more information is lost, the more the KL Divergence.
For classification, however, using KL divergence is the same as minimizing cross entropy (proved below):
Thus, it is recommended to use cross-entropy loss directly.
That said, KL divergence is widely used in many other algorithms:
As a loss function in the t-SNE algorithm. We discussed it here: t-SNE article.
For model compression using knowledge distillation. We discussed it here: Model compression article.
A couple of months back, I also published an algorithm-wise loss function summary, which you can read in this issue: An Algorithm-wise Summary of Loss Functions in Machine Learning.
👉 Over to you: What other common loss functions have I missed?
👉 If you liked this post, don’t forget to leave a like ❤️. It helps more people discover this newsletter on Substack and tells me that you appreciate reading these daily insights.
The button is located towards the bottom of this email.
Thanks for reading!
Latest full articles
If you’re not a full subscriber, here’s what you missed last month:
DBSCAN++: The Faster and Scalable Alternative to DBSCAN Clustering
Federated Learning: A Critical Step Towards Privacy-Preserving Machine Learning
You Cannot Build Large Data Projects Until You Learn Data Version Control!
Sklearn Models are Not Deployment Friendly! Supercharge Them With Tensor Computations.
Deploy, Version Control, and Manage ML Models Right From Your Jupyter Notebook with Modelbit
Gaussian Mixture Models (GMMs): The Flexible Twin of KMeans.
To receive all full articles and support the Daily Dose of Data Science, consider subscribing:
👉 Tell the world what makes this newsletter special for you by leaving a review here :)
👉 If you love reading this newsletter, feel free to share it with friends!





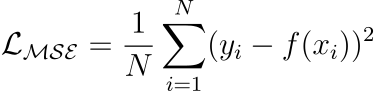







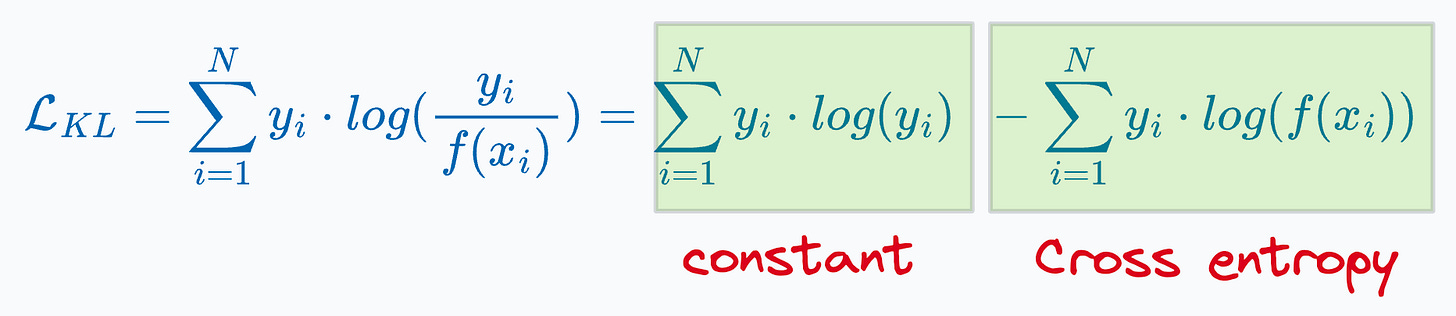

Lovely, Avi :)
Do you have a summary of when it is best to apply each of these loss functions so that we can apply it to real-world scenarios?