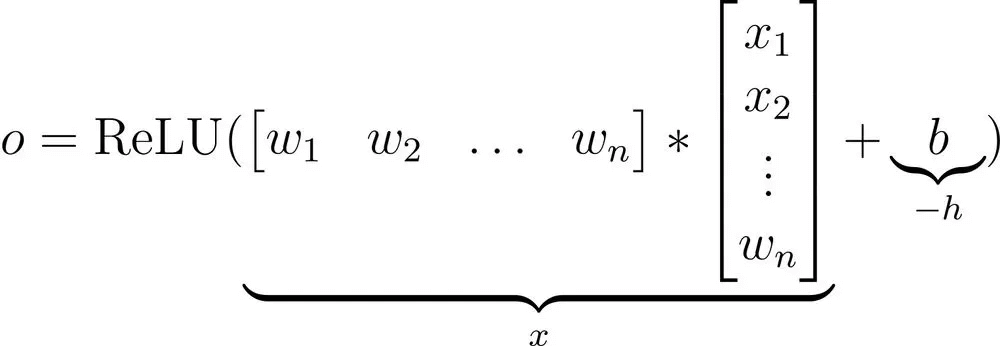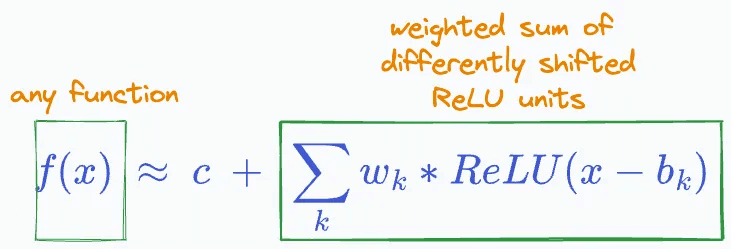An Intuitive Guide to Non-Linearity of ReLU

Exactly why ReLU is a non-linear activation function.

Postman’s Collection Runs to streamline API workflows

Most teams still test APIs one request at a time, which makes it difficult to validate workflows, test functionality, or replicate real user behavior.

Postman’s Collection Runner solves that.

It lets you run API requests in sequence, manually or on a schedule, so you can automate checks, test complete workflows, and simulate how your API behaves under real conditions.

If you want a faster, more reliable way to validate your API workflows, you can try running collections here →

Thanks to Postman for partnering today!

---

An Intuitive Guide to Non-Linearity of ReLU

Many ML engineers struggle to intuitively understand how ReLU adds non-linearity to a neural network because, with its seemingly linear shape, calling it a non-linear activation function isn’t that intuitive.

Today, let’s discuss an intuitive explanation of this!

---

This is the mathematical expression of the ReLU activation function:

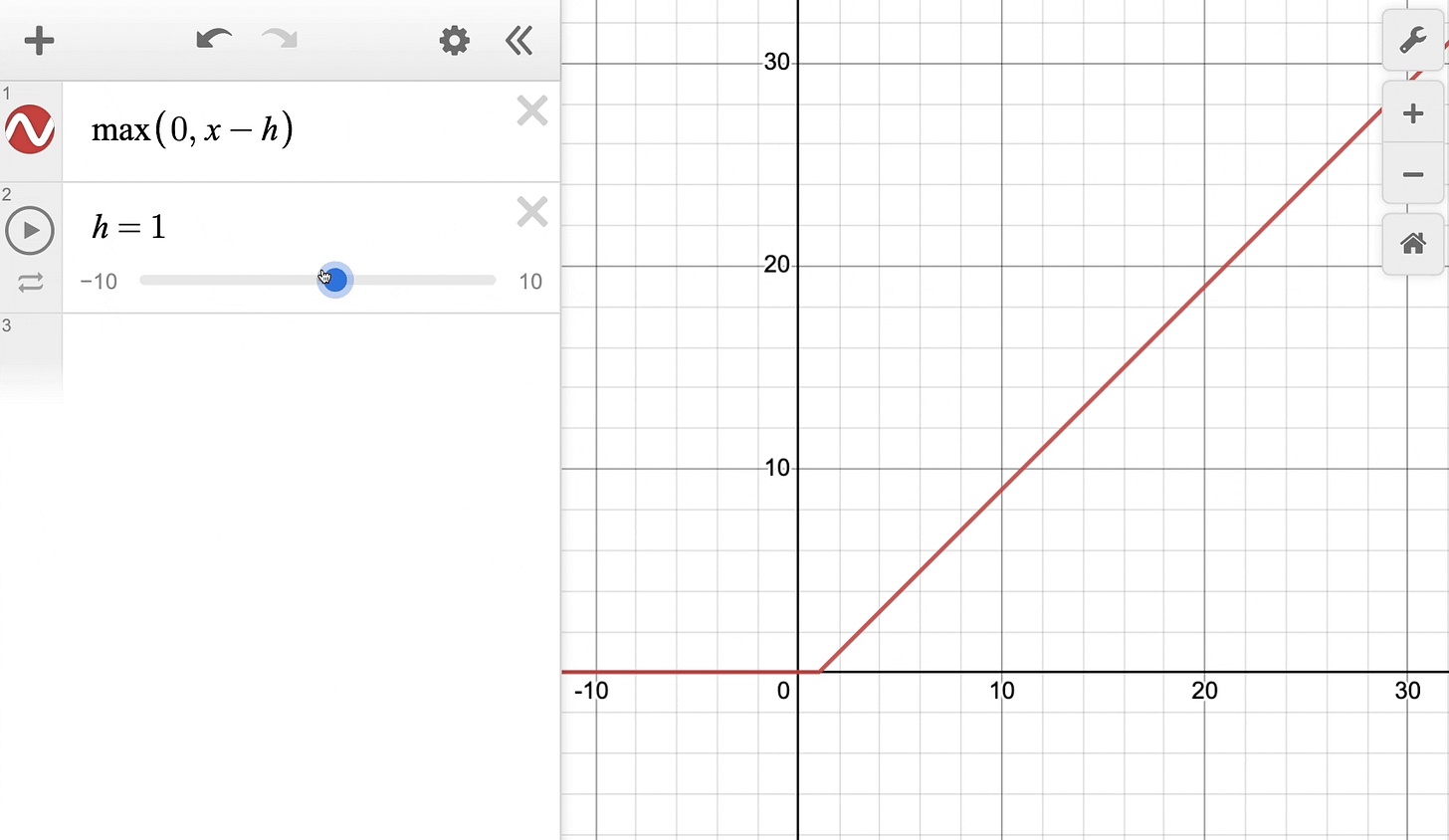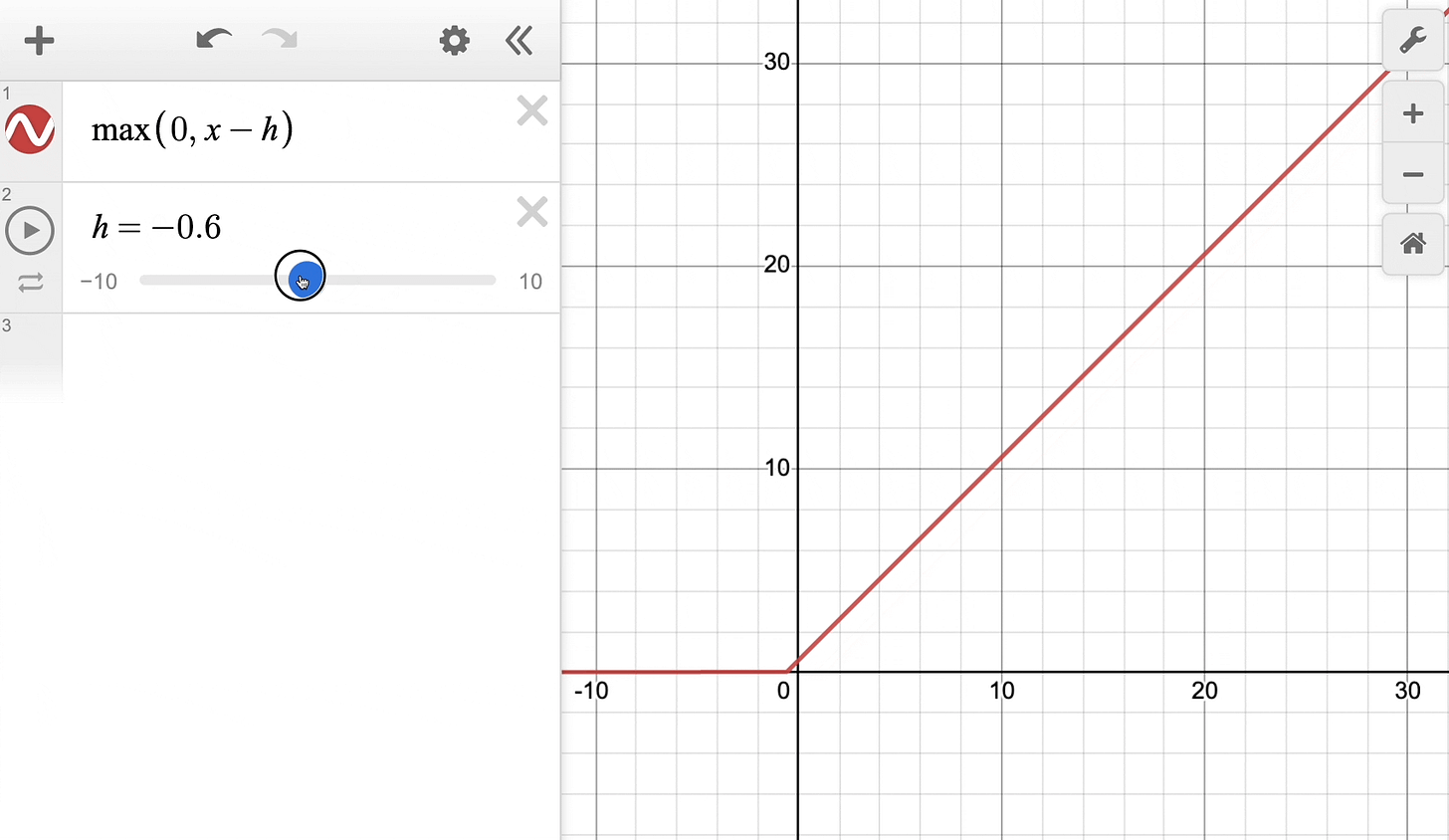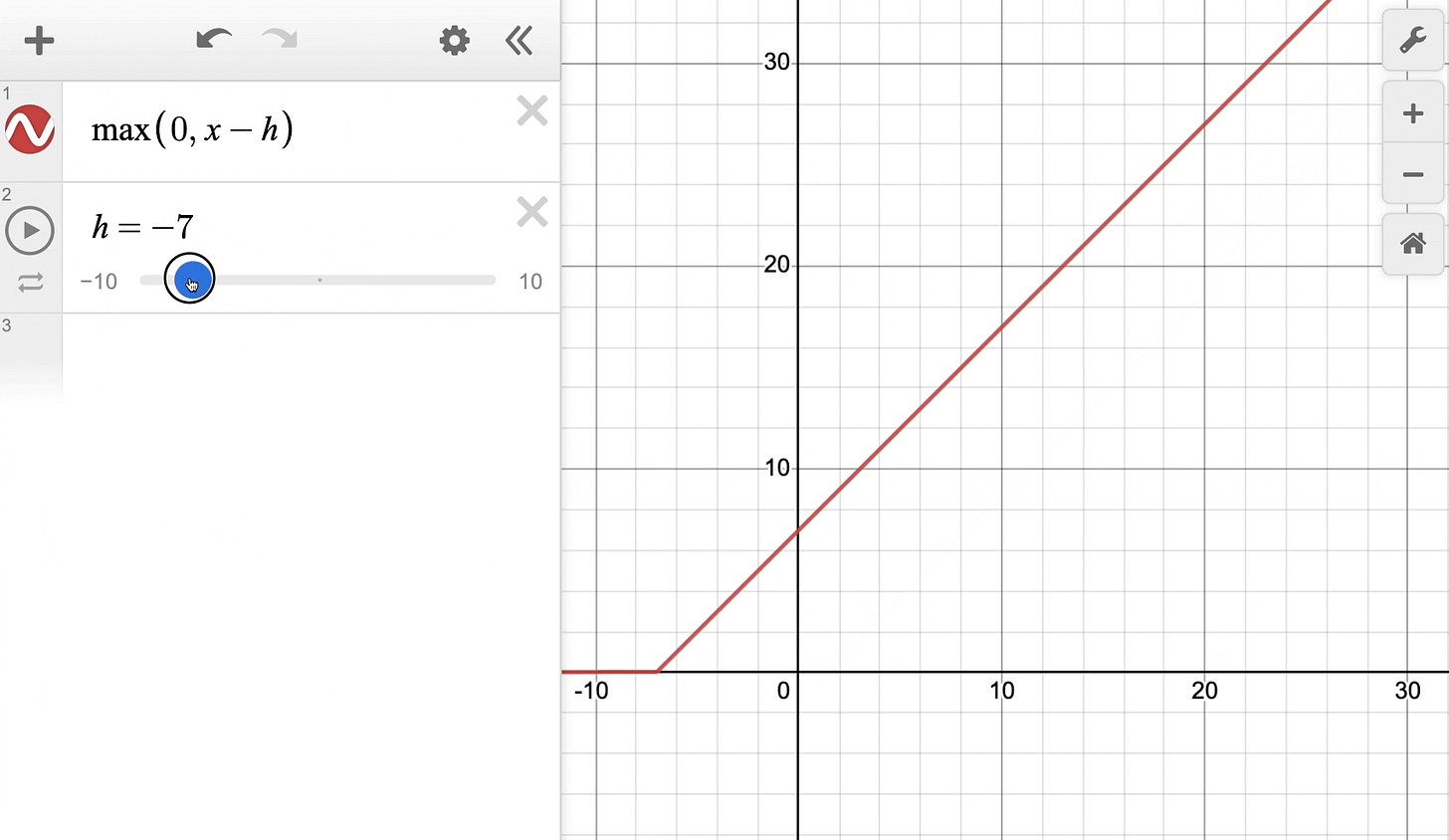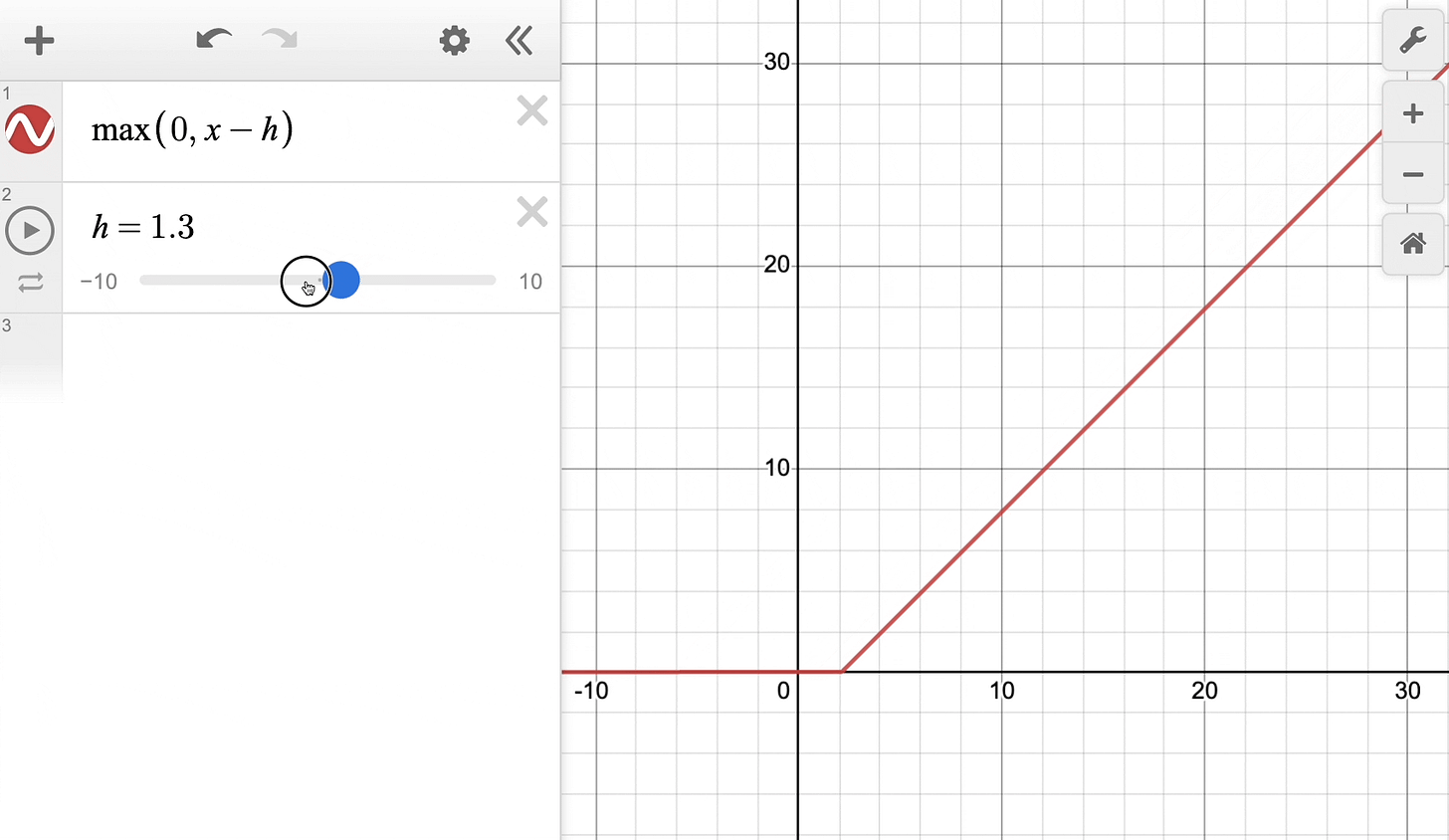
The above definition can be rewritten with a parameter h as follows:

Effectively, it’s the same ReLU function but shifted h units to the right:

Keep this in mind as we’ll return to it shortly.

---

Breaking down a neuron’s output

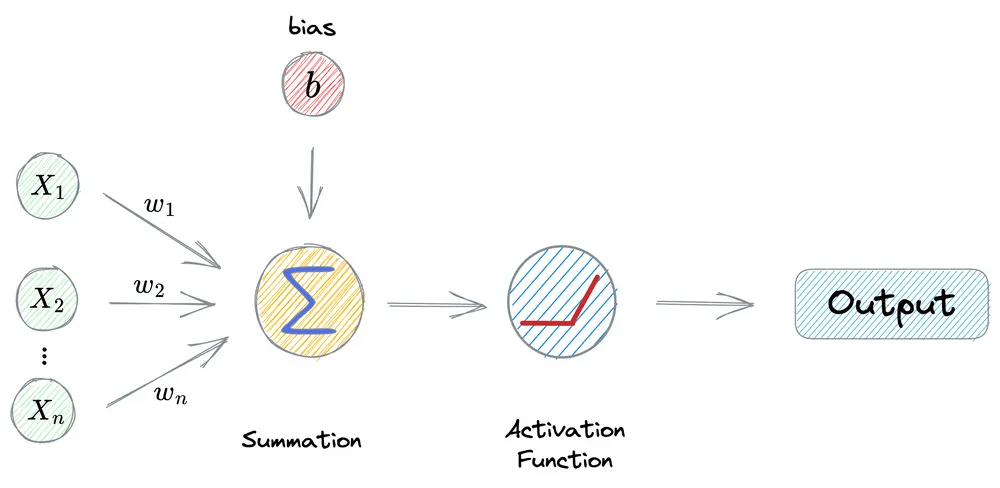
Consider the operations carried out in a neuron:

• First, we have input from the previous layer (x₁, x₂, …, xₙ).

• This is multiplied element-wise by the weights (w₁, w₂, …, wₙ).

• Next, the bias term (b) is added, and every neuron has its own bias term.

• The above output is passed through ReLU activation function to get its output activation.

This final output activation of a neuron is analogous to the ReLU(x−h) function discussed above.

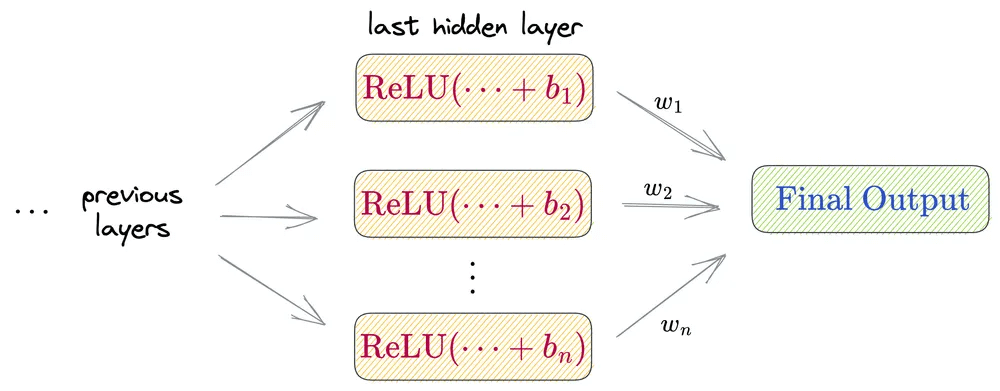
Now, consider all neurons in the last hidden layer:

The final output of the whole network will be a weighted sum of differently shifted ReLU activations computed in the last hidden layer.

---

Plotting dummy ReLU units

Now, let’s plot the weighted sum of some differently shifted ReLU functions to see what this plot looks like.

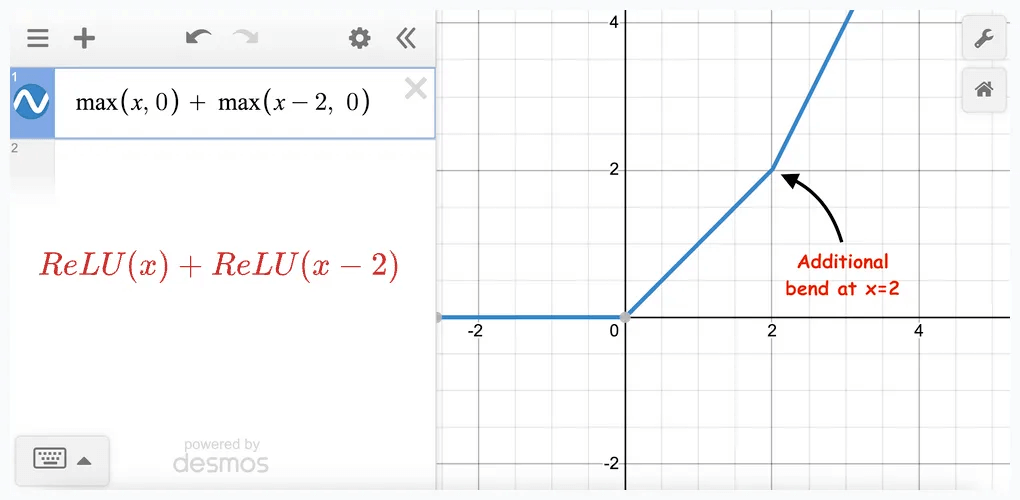
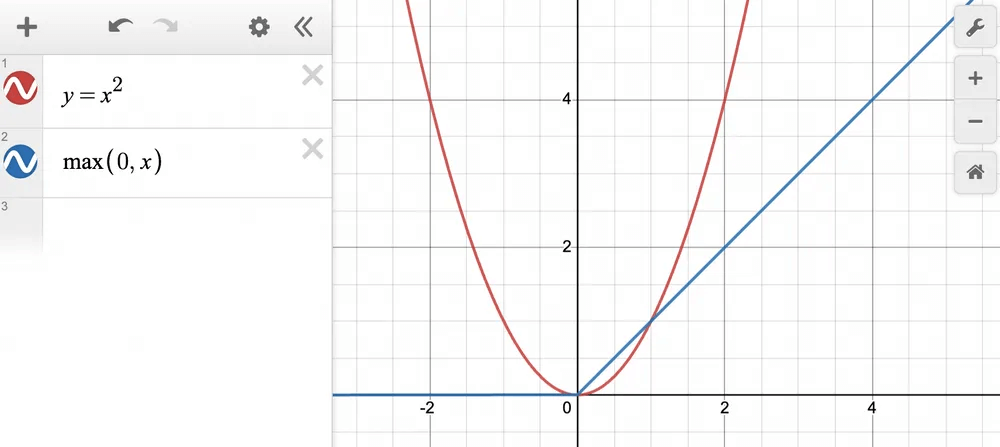
Starting with two terms, we notice a change in slope at a point:

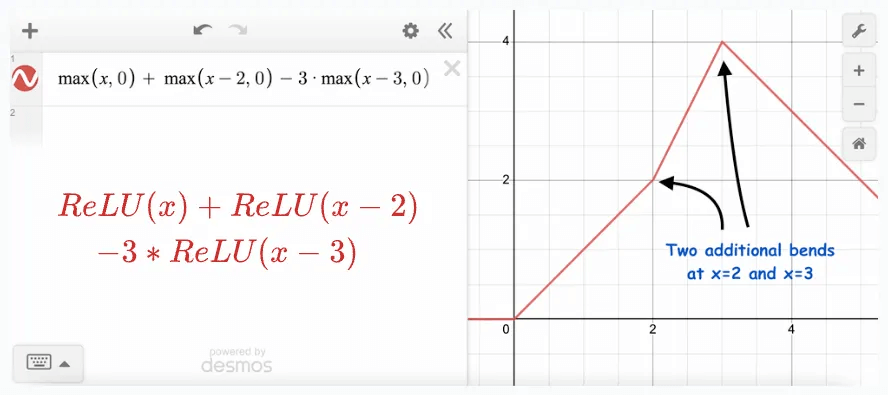
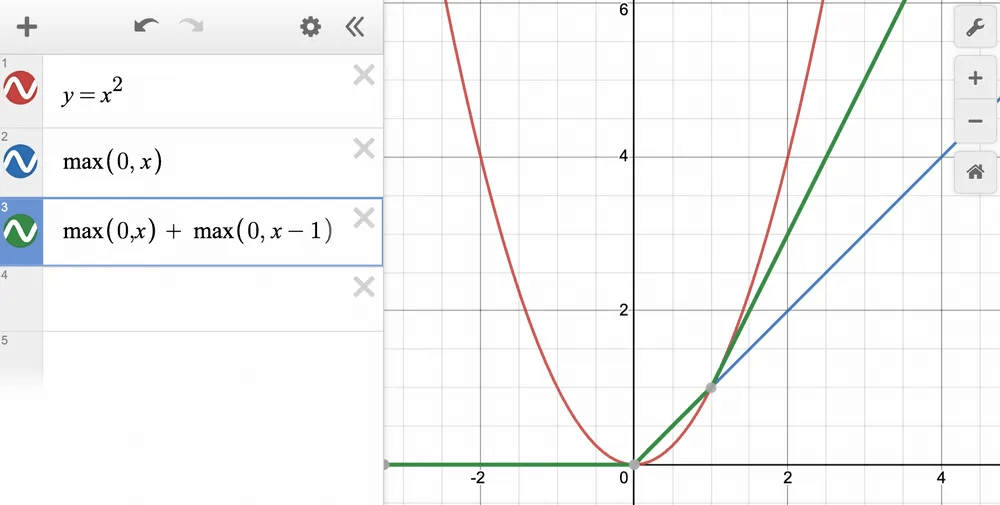
Adding more ReLU terms to this results in more bends:

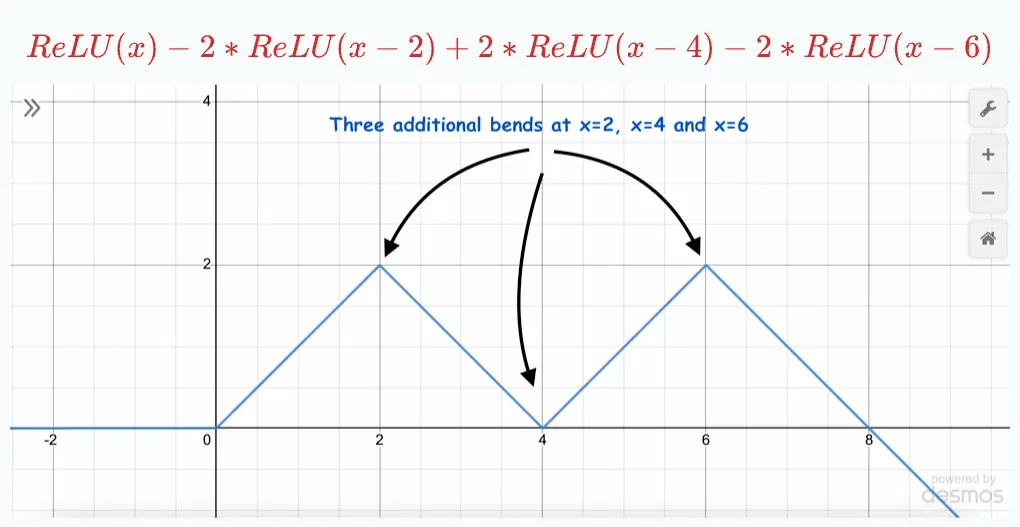
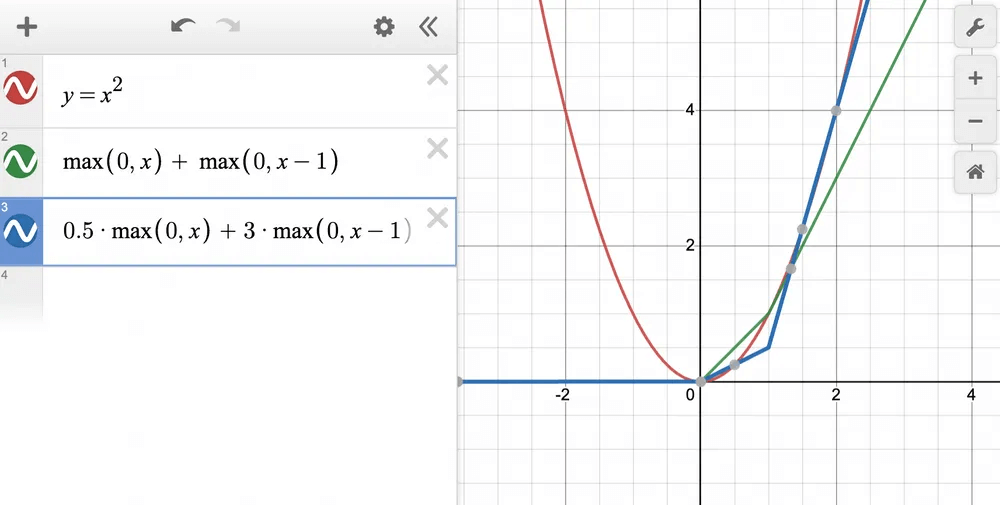
And adding one more produces one more bend:

This indicates we can add more and more ReLU terms, each shifted and multiplied by some constant, to estimate any function, linear or non-linear:

The task is to find those specific weights (w₁, w₂, …, wₙ) which closely estimate the function f(x).

Theoretically, the precision of approximation will be perfect if we add a ReLU term for each possible value of x.

---

X-squared demo

Let’s say we want to approximate y=x^2 for all x ∈ [0,2].

Approximating with just one ReLU term → ReLU(x), we get:

Next, we add another ReLU term and plot ReLU(x) + ReLU(x−1), which produces the green line below and it is a better approximation:

Next, by adjusting the weights, we get the blue line, which approximates this even more precisely:

---

This is exactly how ReLU induces non-linearity in a neural network.

That said, ReLU NEVER adds perfect non-linearity to a neural network. Instead, it’s the piecewise linearity of ReLU that gives us a perception of a non-linear curve.

Also, as we saw above, the strength of ReLU lies not in itself but in an entire army of ReLUs embedded in the network.

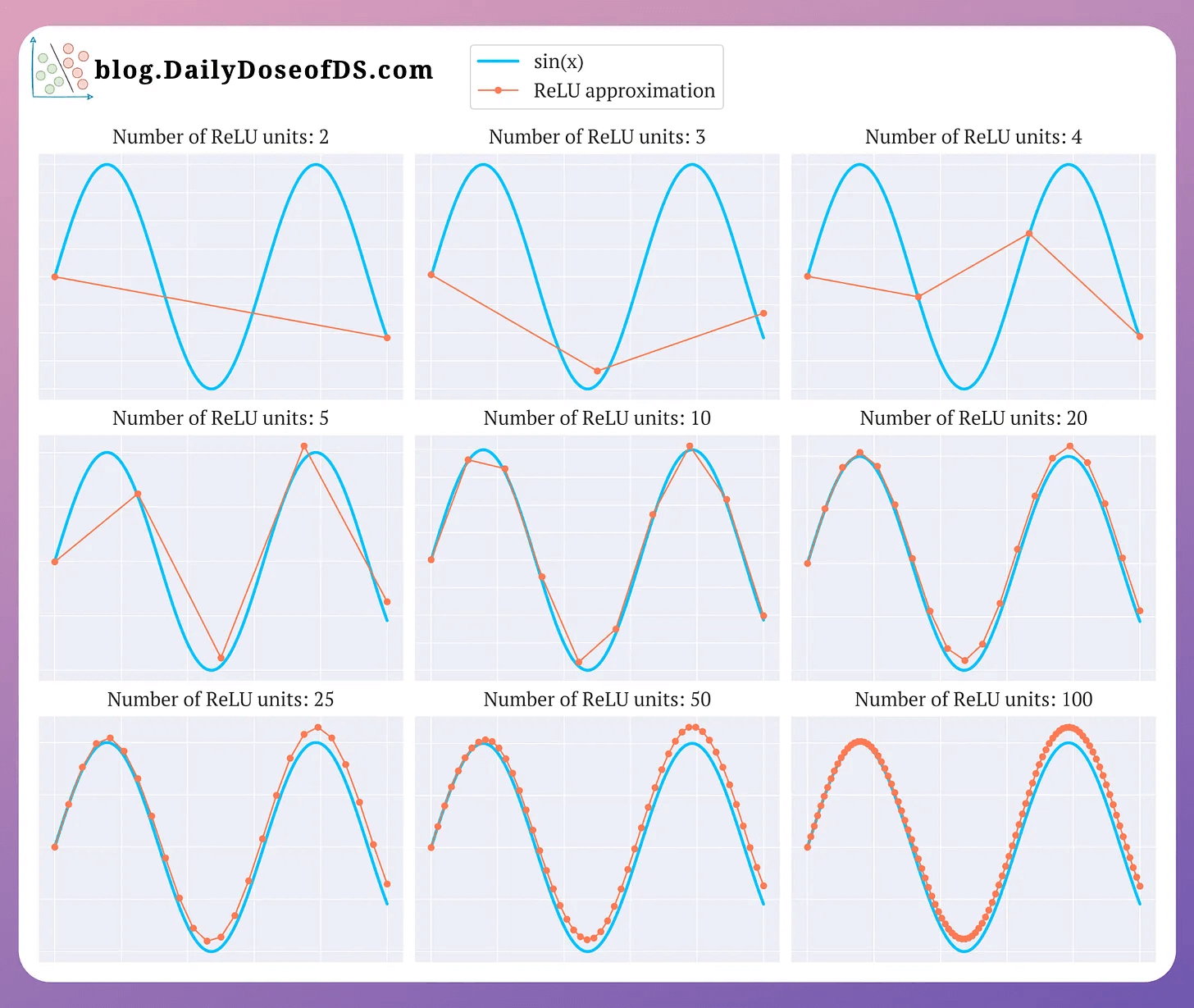
This is why having a few ReLU units in a network may not yield satisfactory results.

This is also evident from the image below, where as the number of ReLU units increases, the approximation also becomes better and at 100 ReLU units, the approximation appears entirely non-linear:

And this is precisely why ReLU is called a non-linear activation function.

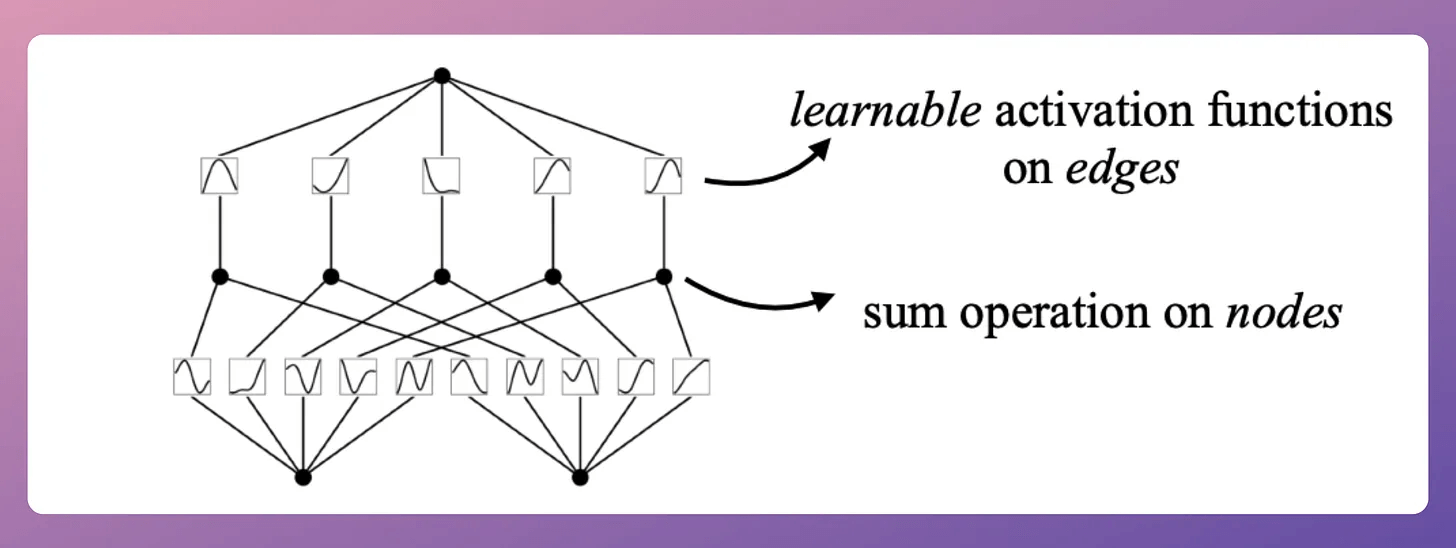
That said, KANs are another popular neural network paradigm that challenges the traditional neural network design and offers an exciting new approach to design and train them:

We did a detailed breakdown and implemented them from scratch here: Implementing KANs From Scratch Using PyTorch.

Thanks for reading!