An Overlooked Technique To Improve KMeans Run-time
Speedup convergence while preserving accuracy.
The standard KMeans algorithm involves a brute-force approach.
To recall, KMeans is trained as follows:
Initialize centroids
Find the nearest centroid for each point
Reassign centroids
Repeat until convergence
As a result, the run-time of KMeans depends on four factors:
Number of iterations (i)
Number of samples (n)
Number of clusters (k)
Number of features (d)
In fact, you can add another factor here — “the repetition factor”, where, we run the whole clustering repeatedly to avoid convergence issues.
But we are ignoring that for now.
While we cannot do much about the first three, reducing the number of features is quite possible, yet often overlooked.
Sparse Random Projection is an efficient projection technique for reducing dimensionality.
Some of its properties are:
It projects the original data to lower dimensions using a sparse random matrix.
It provides similar embedding quality while being memory and run-time efficient.
The similarity and dissimilarity between points are well preserved.
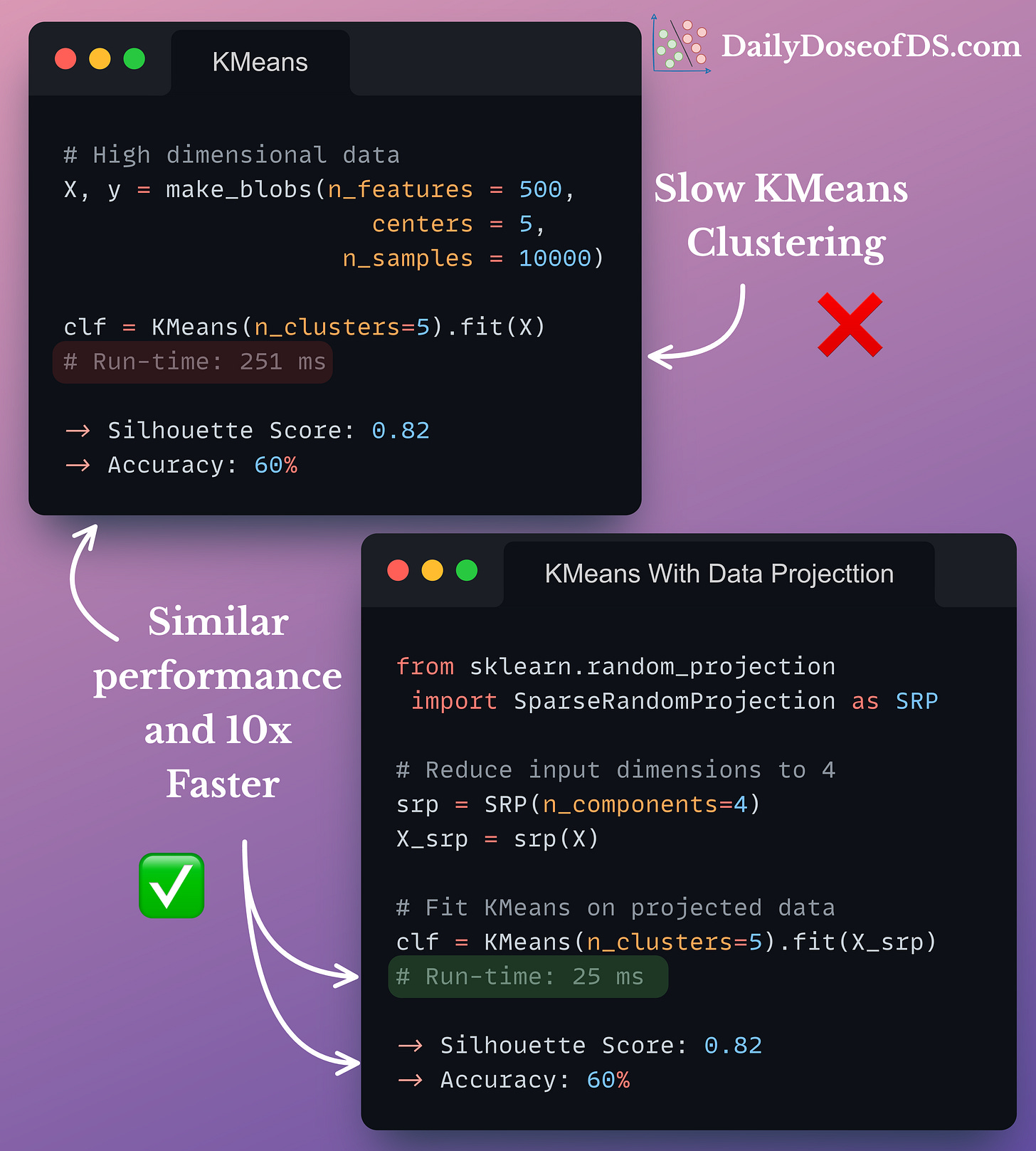
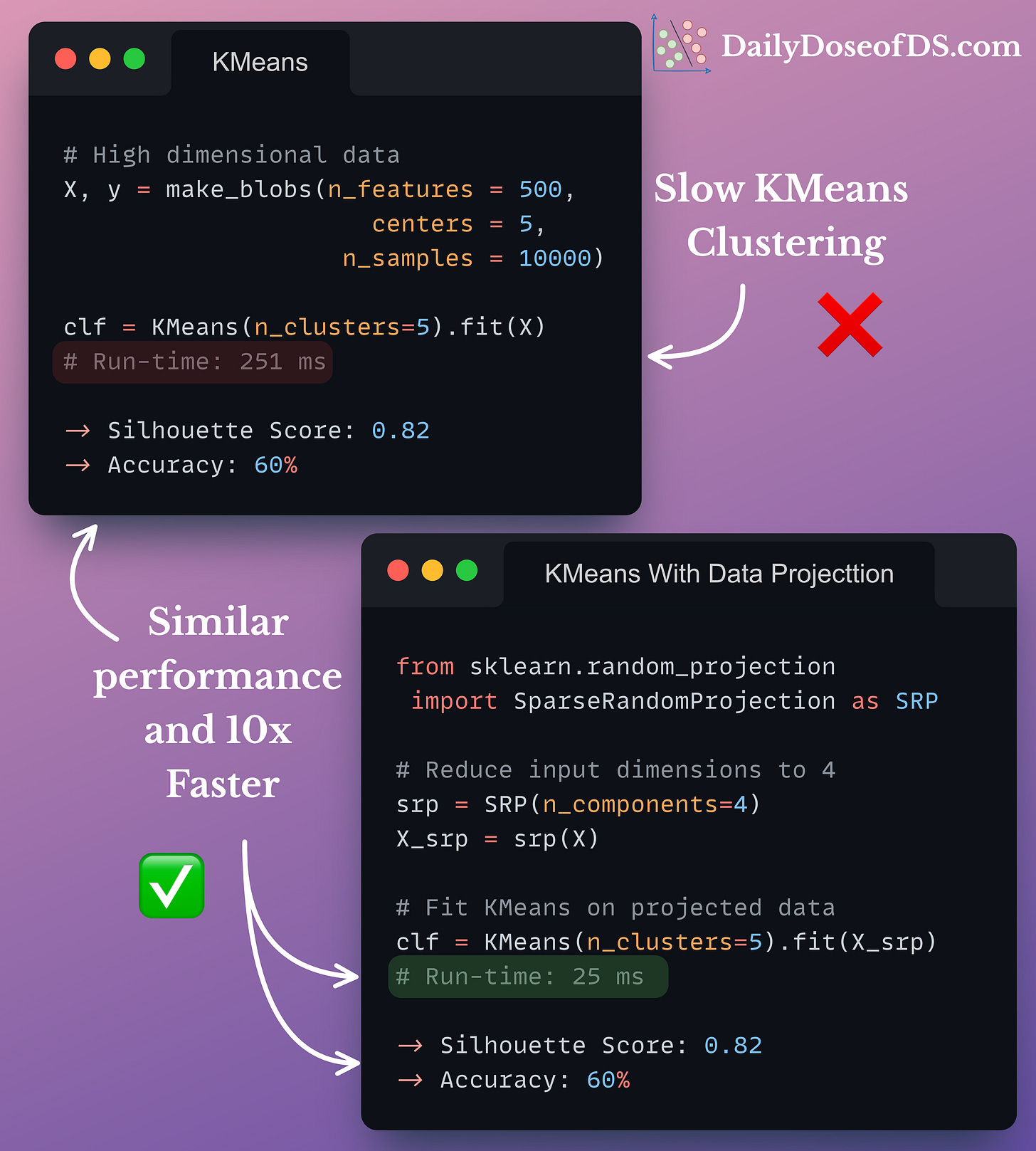
The visual below shows the run-time comparison of KMeans on:
Standard high-dimensional data, vs.
Data projected to lower dimensions using Sparse Random Projection.
As shown, Sparse Random Projection provides:
Similar performance, and
a MASSIVE run-time improvement of 10x.
This can be especially useful in high-dimensional datasets.
Get started with Sparse Random Projections here: Sklearn Docs.
For more info, here’s the paper that discussed it: Very Sparse Random Projections.
👉 Over to you: What are some other ways to improve KMeans run-time?
👉 If you liked this post, don’t forget to leave a like ❤️. It helps more people discover this newsletter on Substack and tells me that you appreciate reading these daily insights. The button is located towards the bottom of this email.
👉 Read what others are saying about this post on LinkedIn and Twitter.
👉 Tell the world what makes this newsletter special for you by leaving a review here :)
👉 If you love reading this newsletter, feel free to share it with friends!
👉 Sponsor the Daily Dose of Data Science Newsletter. More info here: Sponsorship details.
Find the code for my tips here: GitHub.
I like to explore, experiment and write about data science concepts and tools. You can read my articles on Medium. Also, you can connect with me on LinkedIn and Twitter.


Well done mate! 👏
Spare random projection (SRP) is a great technique in terms of speed and also in terms of computational sources.
Because SPR is a way of doing matrix multiplication, it doesn't require Computation and doesn't "consume a lot of RAM" so it's a good choice in general without worrying about the computational resource.
But if we're talking about accuracy, I am not sure that SPR is a good choice here, and I would really prefer using PCA instead of it. Since SPR is based on a randomized algorithm, its output can vary with the same input. While PCA is a deterministic algorithm, it will always give the same output for the same input.
Finally, the dimension reduction technique has a lot of in-depth details to go in.