An Overly Simplified Guide To Understanding How Neural Networks Handle Linearly Inseparable Data
Intuitive guide to handling non-linearity with neural networks.
Many folks struggle to truly comprehend how a neural network learns complex non-linear patterns.
Here’s an intuitive explanation to understand the data transformations performed by a neural network when modeling linearly inseparable data.
We know that in a neural network, the data is passed through a series of transformations at every hidden layer.
This involves:
Linear transformation of the data obtained from the previous layer
…followed by a non-linearity using an activation function — ReLU, Sigmoid, Tanh, etc.
This is depicted below:
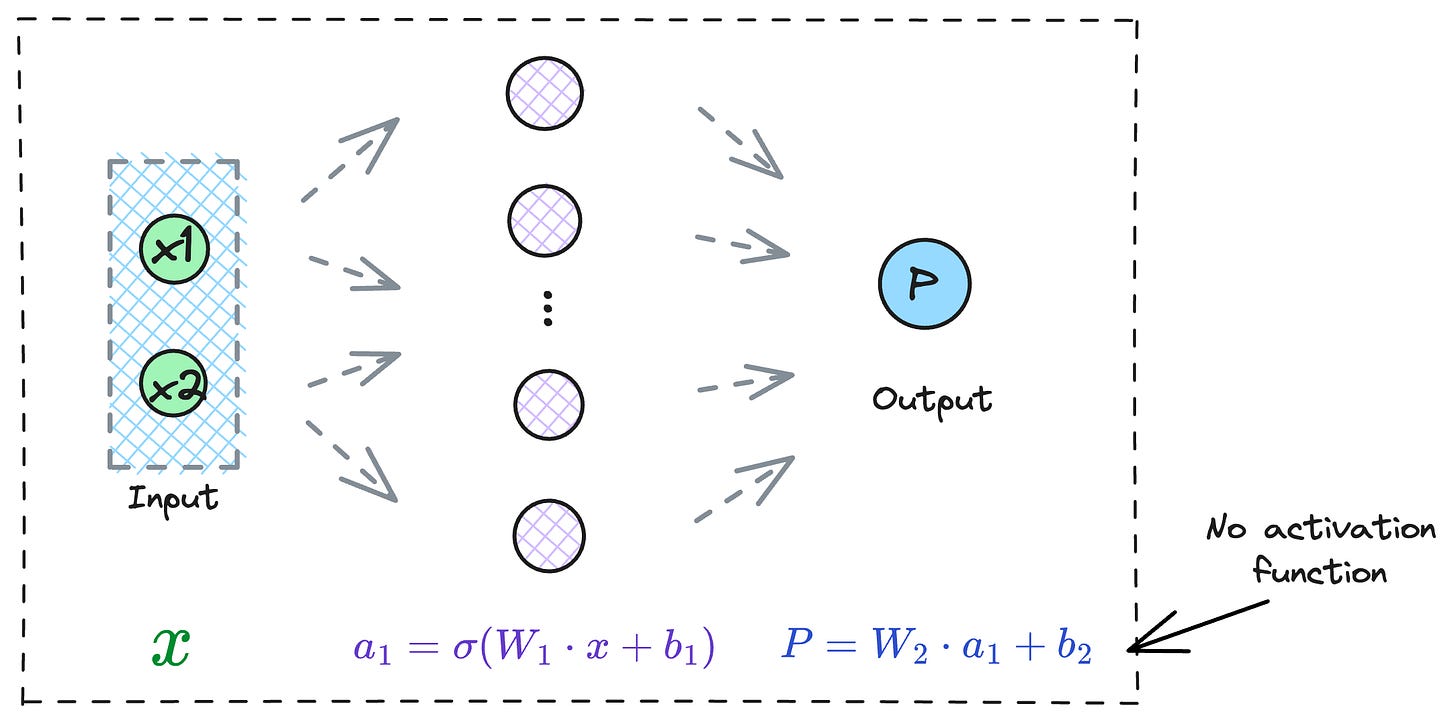
For instance, consider a neural network with just one hidden layer:
The data is transformed at the hidden layer along with an activation function.
Lastly, the output of the hidden layer is transformed to obtain the final output.
It’s time to notice something here.
When the data comes out of the last hidden layer, and it is progressing towards the output layer for another transformation, EVERY activation function that ever existed in the network has already been utilized.
In other words, in any neural network, all sources of non-linearity — “activation functions”, exist on or before the last hidden layer.
And while progressing from the last hidden layer to the output layer, the data will pass through one final transformation before it spits some output.
But given that the transformation from the last hidden layer to the output layer is entirely linear (or without any activation function), there is no further scope for non-linearity in the network.
On a side note, the transformation from the last hidden layer to the output layer (assuming there is only one output neuron) can be thought of as a:
linear regression model for regression tasks, or,
logistic regression if you are modeling class probability with sigmoid function.
Thus, to make accurate predictions, the data received by the output layer from the last hidden layer MUST BE linearly separable.
To summarize…
While transforming the data through all its hidden layers and just before reaching the output layer, a neural network is constantly hustling to project the data to a latent space where it becomes linearly separable.
Once it does, the output layer can easily handle the data.
We can also verify this experimentally.
To visualize the input transformation, add a dummy hidden layer with just two neurons right before the output layer and train the neural network again.
Why two neurons?
It’s simple.
So that we can visualize it easily.
We expect that if we plot the activations of this 2D dummy hidden layer, they should be linearly separable.
The below visual precisely depicts this.
As we notice above, while the input data was linearly inseparable, the input received by the output layer is indeed linearly separable.
This transformed data can be easily handled by the output classification layer.
Hope that helped!
Feel free to respond with any queries that you may have.
👉 If you wish to experiment yourself, the code is available here: Notebook.
👉 If you liked this post, don’t forget to leave a like ❤️. It helps more people discover this newsletter on Substack and tells me that you appreciate reading these daily insights. The button is located towards the bottom of this email.
👉 Tell the world what makes this newsletter special for you by leaving a review here :)
👉 If you love reading this newsletter, feel free to share it with friends!
I like to explore, experiment and write about data science concepts and tools. You can read my articles on Medium. Also, you can connect with me on LinkedIn and Twitter.