Are You Misinterpreting the Purpose of Feature Scaling and Standardization?
Understanding scaling and standardization from the perspective of skewness.
Feature scaling and standardization are two common ways to alter a feature’s range.
For instance:
MinMaxScaler changes the range of a feature to [0,1]:
Standardization makes a feature’s mean zero and standard deviation one:
As you may already know, these operations are necessary because:
They prevent a specific feature from strongly influencing the model’s output.
They ensure that the model is more robust to wide variations in the data.
For instance, in the image below, the scale of “income” could massively impact the overall prediction.
Scaling (or standardizing) the data to a similar range can mitigate this and improve the model’s performance.
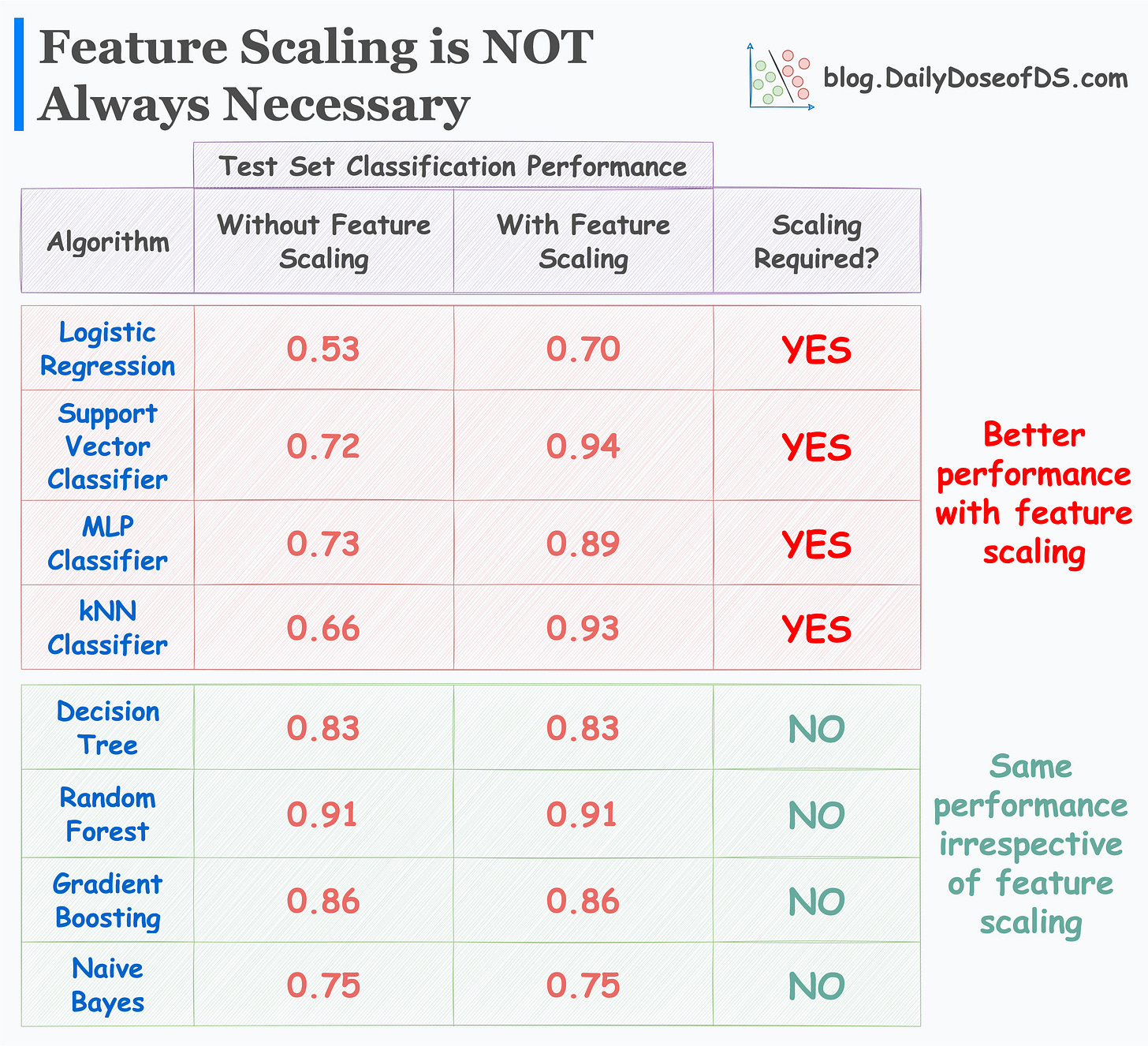
In fact, the following image (taken from one of my previous posts) precisely verifies this:
As depicted above, feature scaling is necessary for the better performance of many ML models.
So while the importance of feature scaling and standardization is pretty clear and well-known, I have seen many people misinterpreting them as techniques to eliminate skewness.
But contrary to this common belief, feature scaling and standardization NEVER change the underlying distribution.
Instead, they just alter the range of values.
Thus, after scaling (or standardization):
Normal distribution → stays Normal
Uniform distribution → stays Uniform
Skewed distribution → stays Skewed
and so on…
We can also verify this from the two illustrations below:
It is clear that scaling and standardization have no effect on the underlying distribution.
Thus, always remember that if you intend to eliminate skewness, scaling/standardization will never help.
Try feature transformations instead.
There are many of them, but the most commonly used transformations are:
Log transform
Sqrt transform
Box-cox transform
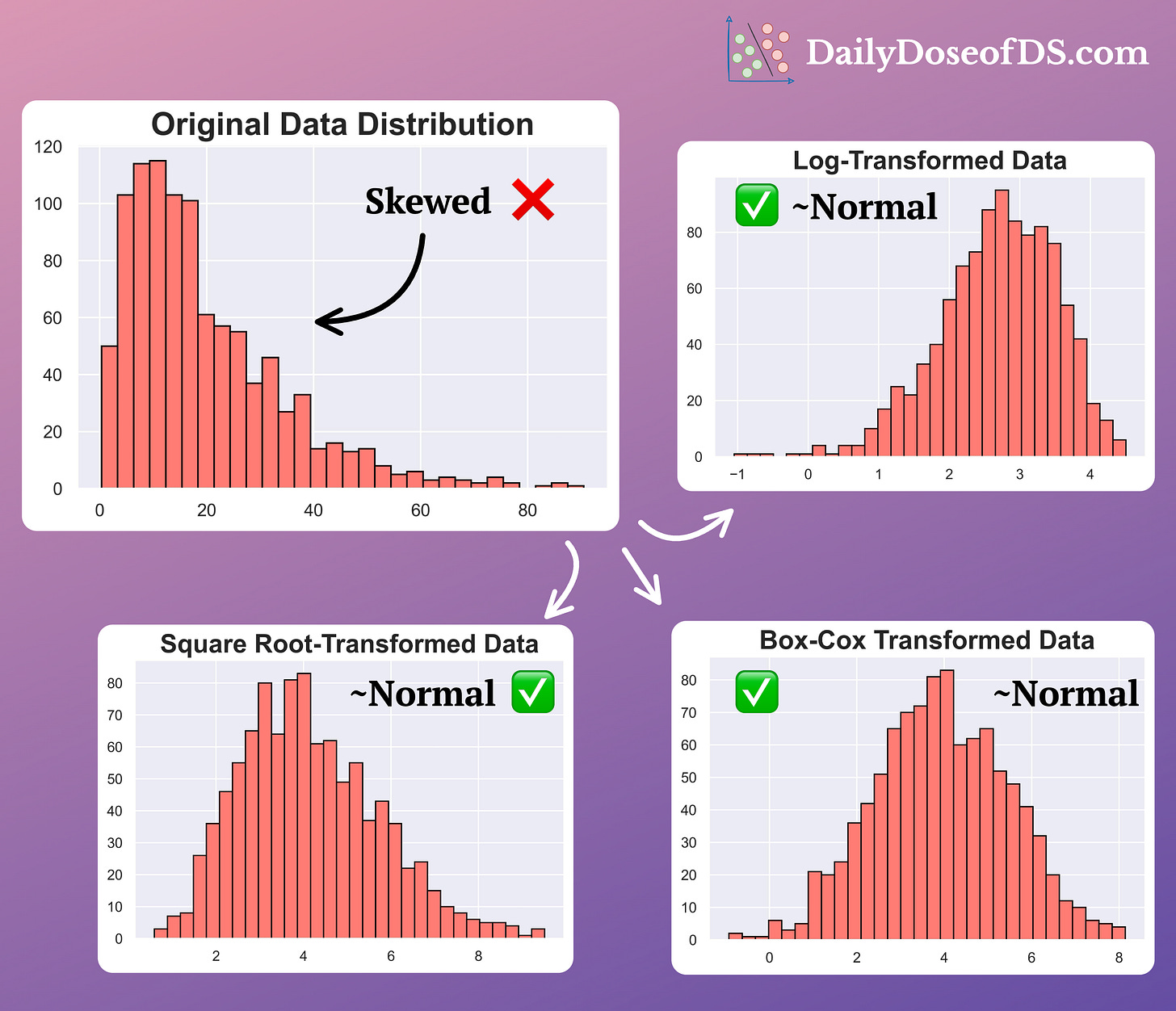
Their effectiveness is evident from the image below:
As depicted above, applying these operations transforms the skewed data into a (somewhat) normally distributed variable.
Before I conclude, please note that while log transform is commonly used to eliminate data skewness, it is not always the ideal solution.
We covered this topic in detail here:
And if you are wondering why did we covert the above-skewed data to a normal distribution, and what was its purpose, then check out this issue:
👉 Over to you: What are some other ways to eliminate skewness?
👉 If you liked this post, don’t forget to leave a like ❤️. It helps more people discover this newsletter on Substack and tells me that you appreciate reading these daily insights.
The button is located towards the bottom of this email.
Thanks for reading!
Latest full articles
If you’re not a full subscriber, here’s what you missed:
DBSCAN++: The Faster and Scalable Alternative to DBSCAN Clustering
Federated Learning: A Critical Step Towards Privacy-Preserving Machine Learning
You Cannot Build Large Data Projects Until You Learn Data Version Control!
Why Bagging is So Ridiculously Effective At Variance Reduction?
Sklearn Models are Not Deployment Friendly! Supercharge Them With Tensor Computations.
Deploy, Version Control, and Manage ML Models Right From Your Jupyter Notebook with Modelbit
Gaussian Mixture Models (GMMs): The Flexible Twin of KMeans.
To receive all full articles and support the Daily Dose of Data Science, consider subscribing:
👉 Tell the world what makes this newsletter special for you by leaving a review here :)
👉 If you love reading this newsletter, feel free to share it with friends!


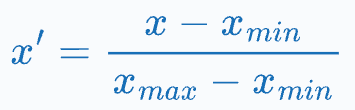






Insightfull
Thank you!