Confidence Interval and Prediction Interval
Here's the difference and what makes them important.
Statistical estimates always have some uncertainty.
For instance, a linear regression model never predicts an actual value.
Consider a simple example of modeling house prices just based on its area. A prediction wouldn’t tell the true value of a house based on its area. This is because different houses of the same size can have different prices.
Instead, what it predicts is the mean value related to the outcome at a particular input. If you read the article on generalized linear models, we discussed it there too.
The point is…
There’s always some uncertainty involved in statistical estimates, and it is important to communicate it.
In this specific case, there are two types of uncertainties:
The uncertainty in estimating the true mean value.
The uncertainty in estimating the true value.
Confidence interval and prediction interval help us capture these uncertainties.
I have often seen people getting confused between the two, so let’s understand this today!
Consider the following dummy dataset:
Let’s fit a linear regression model using statsmodel and print a part of the regression summary:
Notice that the coefficient of the predictor “x1” is 2.0503 with a 95% interval of [1.872, 2.228].
It is a 95% interval because 0.975-0.025 = 0.95.
This is known as the confidence interval, which comes from sampling uncertainty.
More specifically, this uncertainty arises because the data we used above for modeling is just a sample of the population.
So, if we gathered more such samples and fit an OLS to each sample, the true coefficient (which we can only know if we had the data for the entire population) would lie 95% of the time in this confidence interval.
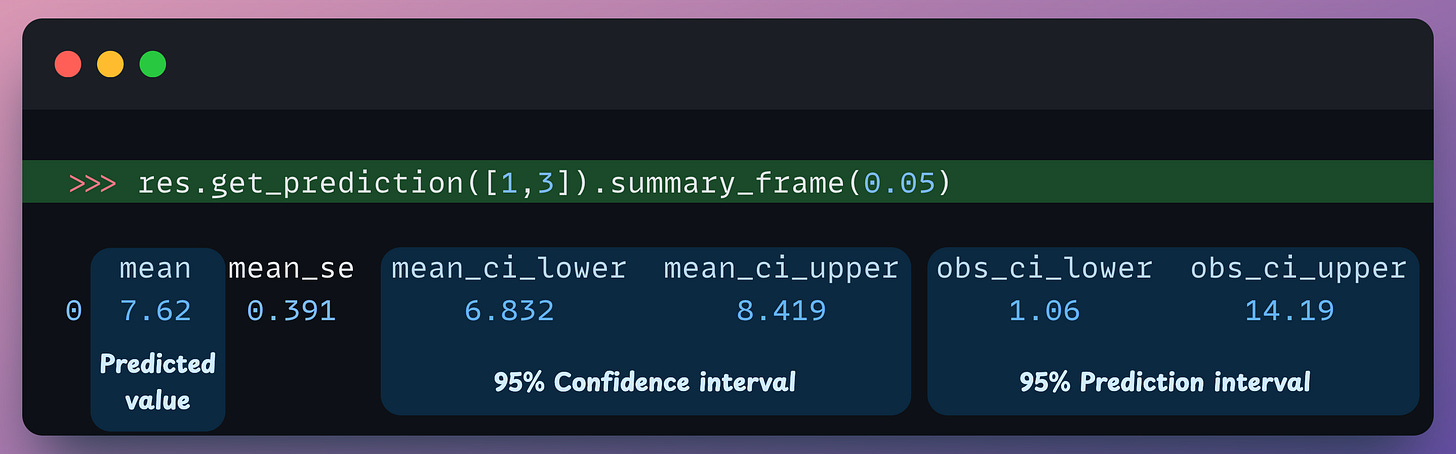
Next, we use this model to make a prediction as follows:
The predicted value is 7.62 (
mean).The 95% confidence interval is [6.832, 8.419].
The 95% prediction interval is [1.06, 14.19].
The confidence interval we saw above was for the coefficient, so what does the confidence interval represent in this case?
Similar to what we discussed above, the data is just a sample of the population.
The regression fit obtained by this sample produced a prediction (some mean value) for the input x=3.
However, if we gathered more such samples and fit an OLS to each dataset, the true mean value (which we can only know if we had the data for the entire population) for this specific input (x=3) would lie 95% of the time in this confidence interval.
Coming to the prediction interval…
…we notice that it is wider than the confidence interval. Why is it, and what does this interval tell?
What we saw above with confidence interval was about estimating the true population mean at a specific input.
What we are talking about now is obtaining an interval where the true value for an input can lie.
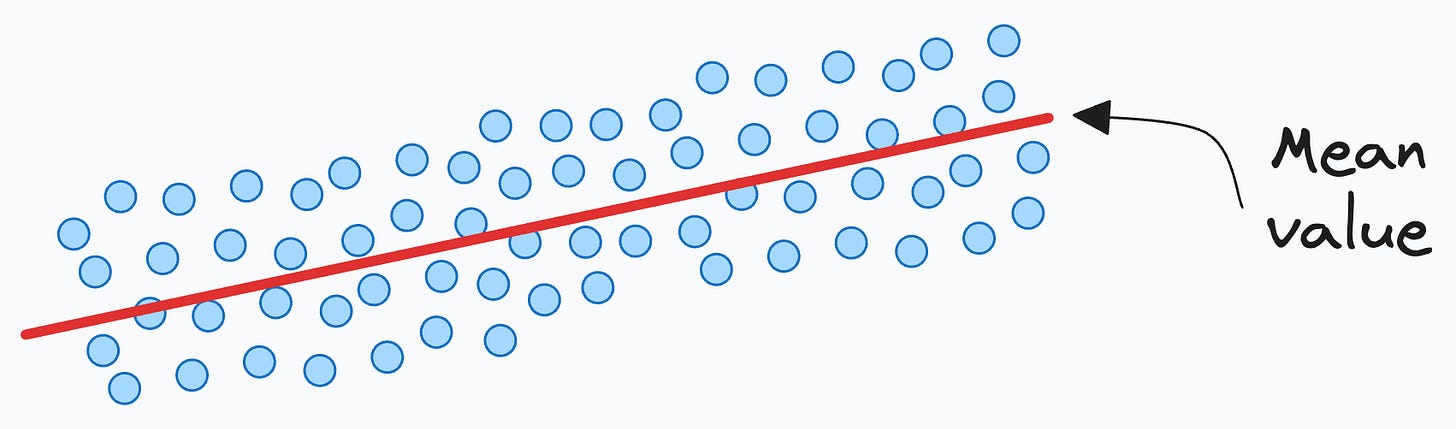
Thus, this additional uncertainty appears because in our dataset, for the same value of input x, there can be multiple different values of the outcome. This is depicted below:
Thus, it is wider than the confidence interval. Plotting it across the entire input range, we get the following plot:
Given that the model is predicting a mean value (as depicted below), we have to represent the prediction uncertainty that the actual value can lie anywhere in the prediction interval:
A 95% prediction interval tells us that we can be 95% sure that the actual value of this observation will fall within this interval.
So to summarize:
A confidence interval captures the sampling uncertainty. More data means less sampling uncertainty, which in turn leads to a smaller interval.
In addition to the sampling uncertainty, the prediction interval also represents the uncertainty in estimating the true value of a particular data point. Thus, it is wider than the confidence interval.
Communicating these uncertainties is quite crucial in decision-making because it provides a clearer understanding of the reliability and precision of predictions.
This transparency allows stakeholders to make more informed decisions by considering the range of possible outcomes and the associated risks.
Other than this, understanding causality is another critical skill for business decision-making. We did a crash course here:
👉 Over to you: What does a 100% confidence interval and prediction interval look like?
Are you overwhelmed with the amount of information in ML/DS?
Every week, I publish no-fluff deep dives on topics that truly matter to your skills for ML/DS roles.
For instance:
A Beginner-friendly Introduction to Kolmogorov Arnold Networks (KANs)
5 Must-Know Ways to Test ML Models in Production (Implementation Included)
Understanding LoRA-derived Techniques for Optimal LLM Fine-tuning
8 Fatal (Yet Non-obvious) Pitfalls and Cautionary Measures in Data Science
Implementing Parallelized CUDA Programs From Scratch Using CUDA Programming
You Are Probably Building Inconsistent Classification Models Without Even Realizing
And many many more.
Join below to unlock all full articles:
SPONSOR US
Get your product in front of 80,000 data scientists and other tech professionals.
Our newsletter puts your products and services directly in front of an audience that matters — thousands of leaders, senior data scientists, machine learning engineers, data analysts, etc., who have influence over significant tech decisions and big purchases.
To ensure your product reaches this influential audience, reserve your space here or reply to this email to ensure your product reaches this influential audience.












Simple explained! Thanks.
Very good!
Thank you very much!