Correlation != Predictiveness
Here’s how to measure predictiveness.
Before I begin…
I met many readers of this newsletter over the last two days to purposefully gather some critical and honest feedback.
My objective is to have a real one-on-one conversation where I get to learn more about you, the problems you have that this newsletter is NOT able to solve, etc.
If you’d be willing to connect for 30 minutes to talk to me, please reply to this email. I’ll share my calendar link with you.
Thank you so much!
Let’s get to today’s post now.
Correlation measures how two features vary with one another linearly (or monotonically).
This makes correlation symmetric: corr(A, B) = corr(B, A).
Yet, associations are often asymmetric.
For instance, given a date, it is easy to tell the month. But given a month, you can never tell the date.
Correlation, being symmetric, entirely ignores this notion.
What’s more, it is not meant to quantify how well a feature can predict the outcome, as demonstrated below:
Yet, at times, it is misinterpreted as a measure of “predictiveness”.
Lastly, correlation is mostly limited to numerical data. But categorical data is equally important for predictive models.
The Predictive Power Score (PPS) addresses each of these limitations.
As the name suggests, it measures the predictive power of a feature.
PPS(a → b) is calculated as follows:
If the target (b) is numeric:
Train a Decision Tree Regressor that predicts b using a.
Find PPS by comparing its MAE to the MAE of a baseline model (median prediction).
If the target (b) is categorical:
Train a Decision Tree Classifier that predicts b using a.
Find PPS by comparing its F1 to the F1 of a baseline model (random or most frequent prediction).
Thus, PPS:
is asymmetric, meaning
PPS(a, b) != PPS(b, a).can be used on categorical targets (b).
can be used to measure the predictive power of categorical features (a).
works well for linear and non-linear relationships.
works well for monotonic and non-monotonic relationships.
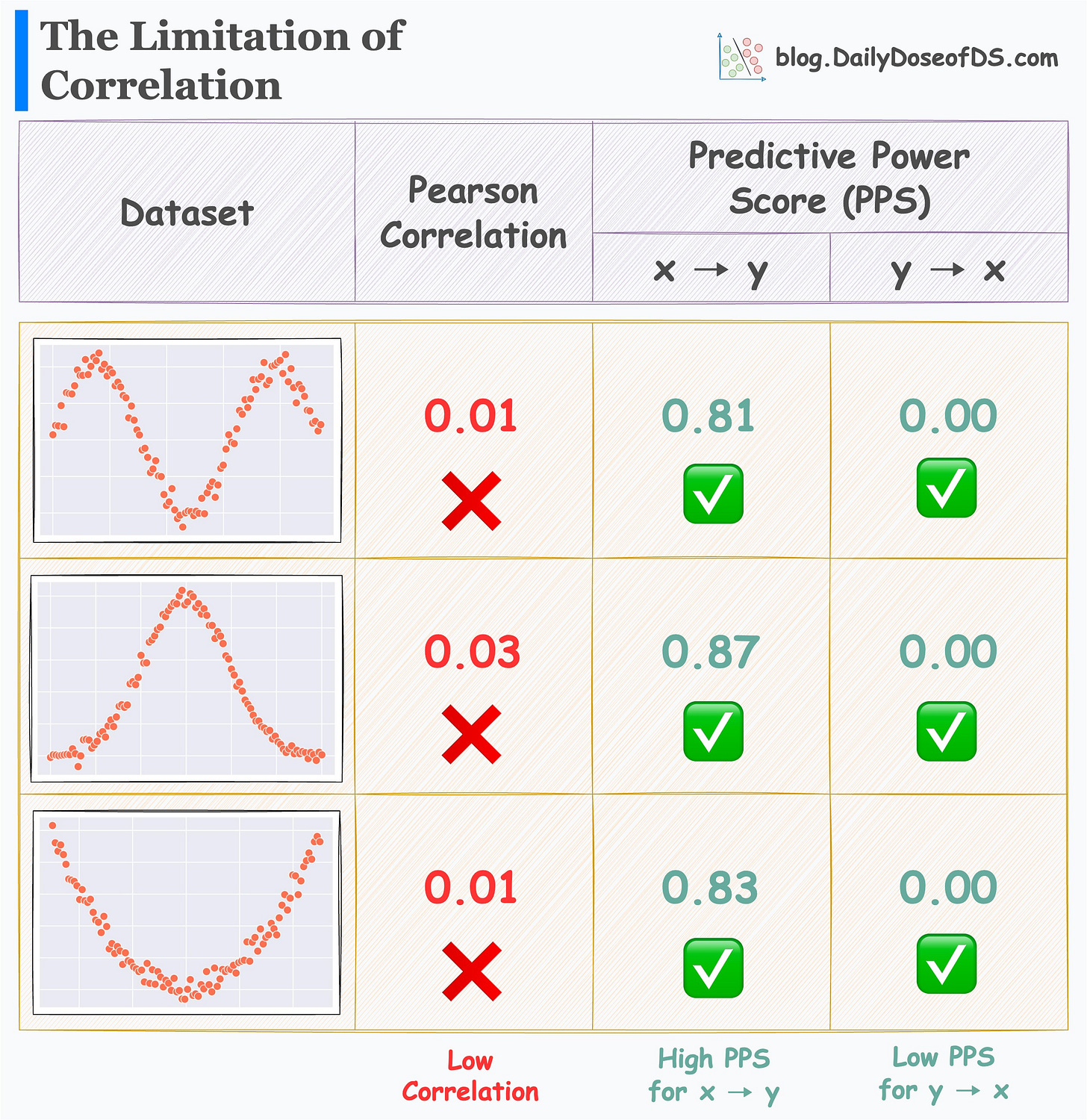
Its effectiveness is evident from the image below.
For all three datasets:
Correlation is low.
PPS (x → y) is high.
PPS (y → x) is zero.
That being said, it is important to note that correlation has its place.
When selecting between PPS and correlation, first set a clear objective about what you wish to learn about the data:
Do you want to know the general monotonic trend between two variables? Correlation will help.
Do you want to know the predictiveness of a feature? PPS will help.
👉 Over to you: What other points will you add here about PPS vs. Correlation?
Get started with PPS: GitHub.
Thanks for reading!
Whenever you are ready, here’s one more way I can help you:
Every week, I publish 1-2 in-depth deep dives (typically 20+ mins long). Here are some of the latest ones that you will surely like:
[FREE] A Beginner-friendly and Comprehensive Deep Dive on Vector Databases.
A Detailed and Beginner-Friendly Introduction to PyTorch Lightning: The Supercharged PyTorch
You Are Probably Building Inconsistent Classification Models Without Even Realizing
Why Sklearn’s Logistic Regression Has no Learning Rate Hyperparameter?
PyTorch Models Are Not Deployment-Friendly! Supercharge Them With TorchScript.
Federated Learning: A Critical Step Towards Privacy-Preserving Machine Learning.
You Cannot Build Large Data Projects Until You Learn Data Version Control!
To receive all full articles and support the Daily Dose of Data Science, consider subscribing:
👉 If you love reading this newsletter, feel free to share it with friends!
👉 Tell the world what makes this newsletter special for you by leaving a review here :)







Are you aware of the distance-correlation? it can describe non-linear correlations. There is also a version of distance-correlation for time series (aka the samples are not iid).