Decision Trees ALWAYS Overfit! Here's a Neat Technique to Prevent It
Balancing cost and model size.
By default, a decision tree (in sklearn’s implementation, for instance), is allowed to grow until all leaves are pure.
This happens because a standard decision tree algorithm greedily selects the best split at each node.
This makes its nodes more and more pure as we traverse down the tree.
As the model correctly classifies ALL training instances, it leads to 100% overfitting, and poor generalization.
For instance, consider this dummy dataset:
Fitting a decision tree on this dataset gives us the following decision region plot:
It is pretty evident from the decision region plot, the training and test accuracy that the model has entirely overfitted our dataset.
Cost-complexity-pruning (CCP) is an effective technique to prevent this.
CCP considers a combination of two factors for pruning a decision tree:
Cost (C): Number of misclassifications
Complexity (C): Number of nodes
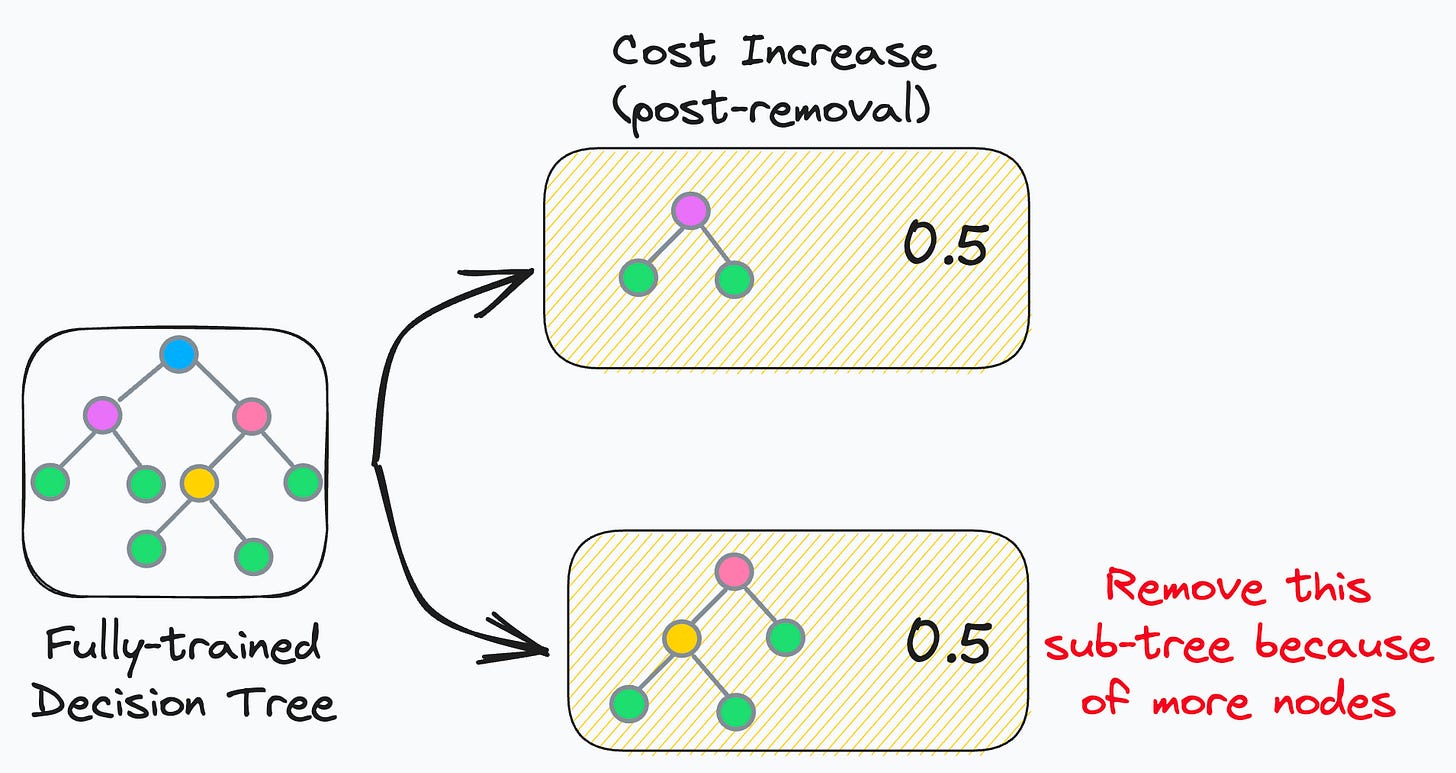
The core idea is to iteratively drop sub-trees, which, after removal, lead to:
a minimal increase in classification cost
a maximum reduction of complexity (or nodes)
In other words, if two sub-trees lead to a similar increase in classification cost, then it is wise to remove the sub-tree with more nodes.
In sklearn, you can control cost-complexity-pruning using the ccp_alpha parameter:
large value of
ccp_alpha→ results in underfittingsmall value of
ccp_alpha→ results in overfitting
The objective is to determine the optimal value of ccp_alpha, which gives a better model.
The effectiveness of cost-complexity-pruning is evident from the image below:
As depicted above, CCP results in a much simpler and acceptable decision region plot.
That said, Bagging is another pretty effective way to avoid this overfitting problem.
The idea (as you may already know) is to:
create different subsets of data with replacement (this is called bootstrapping)
train one model per subset
aggregate all predictions to get the final prediction
As a result, it drastically reduces the variance of a single decision tree model, as shown below:
While we can indeed verify its effectiveness experimentally (as shown above), most folks struggle to intuitively understand:
Why Bagging is so effective.
Why do we sample rows from the training dataset with replacement.
How to mathematically formulate the idea of Bagging and prove variance reduction.
Can you answer these questions?
If not, we covered this in full detail here: Why Bagging is So Ridiculously Effective At Variance Reduction?
The article dives into the entire mathematical foundation of Bagging, which will help you:
Truly understand and appreciate the mathematical beauty of Bagging as an effective variance reduction technique
Why the random forest model is designed the way it is.
👉 Over to you: What are some other ways you use to prevent decision trees from overfitting?
👉 If you liked this post, don’t forget to leave a like ❤️. It helps more people discover this newsletter on Substack and tells me that you appreciate reading these daily insights.
The button is located towards the bottom of this email.
Thanks for reading!
Latest full articles
If you’re not a full subscriber, here’s what you missed last month:
PyTorch Models Are Not Deployment-Friendly! Supercharge Them With TorchScript.
How To (Immensely) Optimize Your Machine Learning Development and Operations with MLflow.
Don’t Stop at Pandas and Sklearn! Get Started with Spark DataFrames and Big Data ML using PySpark.
DBSCAN++: The Faster and Scalable Alternative to DBSCAN Clustering.
Federated Learning: A Critical Step Towards Privacy-Preserving Machine Learning.
You Cannot Build Large Data Projects Until You Learn Data Version Control!
Deploy, Version Control, and Manage ML Models Right From Your Jupyter Notebook with Modelbit.
To receive all full articles and support the Daily Dose of Data Science, consider subscribing:
👉 Tell the world what makes this newsletter special for you by leaving a review here :)
👉 If you love reading this newsletter, feel free to share it with friends!