The Must-Know Categorisation of Discriminative Models

A popular interview question.

In one of the earlier posts, we discussed Generative and Discriminative Models.

Today’s post dives into a further categorization of discriminative models.

Let’s understand.

To recap:

Discriminative models:

• learn decision boundaries that separate different classes.

• maximize the conditional probability: P(Y|X) — Given an input X, maximize the probability of label Y.

• are meant explicitly for classification tasks.

Generative models:

• maximize the joint probability: P(X, Y)

• learn the class-conditional distribution P(X|Y)

• are typically not meant for classification tasks, but they can perform classification nonetheless.

---

In a gist, discriminative models directly learn the function f that maps an input vector (x) to a label (y).

They can be further divided into two categories:

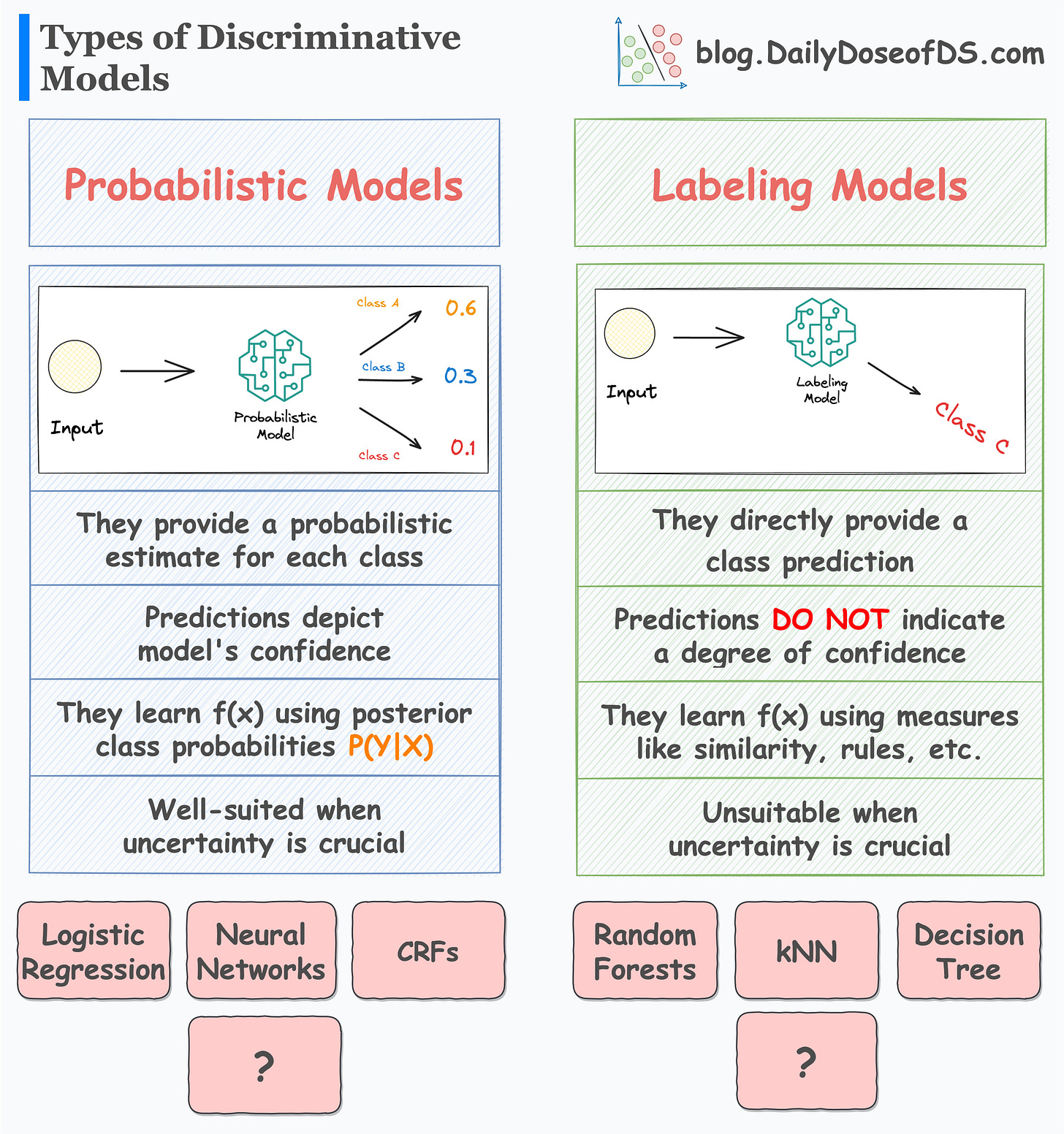
• Probabilistic models

• Direct labeling models

Probabilistic models

Probabilistic models

As the name suggests, probabilistic models provide a probabilistic estimate for each class.

They do this by learning the posterior class probabilities P(Y|X).

As a result, their predictions depict the model’s confidence in predicting a specific class label.

This makes them well-suited in situations when uncertainty is crucial to the problem at hand.

Examples include:

• Logistic regression

• Neural networks

• Conditional Random Fields (CRFs)

Labeling models

Labeling models

In contrast to probabilistic models, labeling models (also called distribution-free classifiers) directly predict the class label — without providing any probabilistic estimate.

As a result, their predictions DO NOT indicate a degree of confidence.

This makes them unsuitable when uncertainty in a model’s prediction is crucial.

Examples include:

• Random forests

• kNN

• Decision trees

That being said, it is important to note that these models, in some way, can be manipulated to output a probability.

For instance, Sklearn’s decision tree classifier does provide a predict_proba() method, as shown below:

This may appear a bit counterintuitive at first.

In this case, the model outputs the class probabilities by looking at the fraction of training class labels in a leaf node.

In other words, say a test instance reaches a specific leaf node for final classification. The model will calculate the probabilities as the fraction of training class labels in that leaf node.

Yet, these manipulations do not account for the “true” uncertainty in a prediction.

This is because the uncertainty is the same for all predictions that land in the same leaf node.

Therefore, it is always wise to choose probabilistic classifiers when uncertainty is paramount.

👉 Over to you: Can you add one more model for probabilistic and labeling models?

👉 If you liked this post, don’t forget to leave a like ❤️. It helps more people discover this newsletter on Substack and tells me that you appreciate reading these daily insights. The button is located towards the bottom of this email.

Thanks for reading :)

---

Whenever you’re ready, here are a couple of more ways I can help you:

• Get the full experience of the Daily Dose of Data Science. Every week, receive two curiosity-driven deep dives that:

  • Make you fundamentally strong at data science and statistics.

  • Help you approach data science problems with intuition.

  • Teach you concepts that are highly overlooked or misinterpreted.

Daily Dose of Data Science ML articles

• Promote to 30,000 subscribers by sponsoring this newsletter.

---

👉 Tell the world what makes this newsletter special for you by leaving a review here :)

👉 If you love reading this newsletter, feel free to share it with friends!