How are QQ Plots Created?
Drawing a QQ plot from scratch.
A QQ plot is a great way to visually assess the similarity between two distributions:
It does this by plotting the quantiles of the two distributions against each other.
The deviations from the straight line indicate the differences between the two distributions.
Have you ever wondered how it is created?
The following visual depicts this:
Let’s discuss it in more detail.
Consider we have two distributions, D1 and D2.
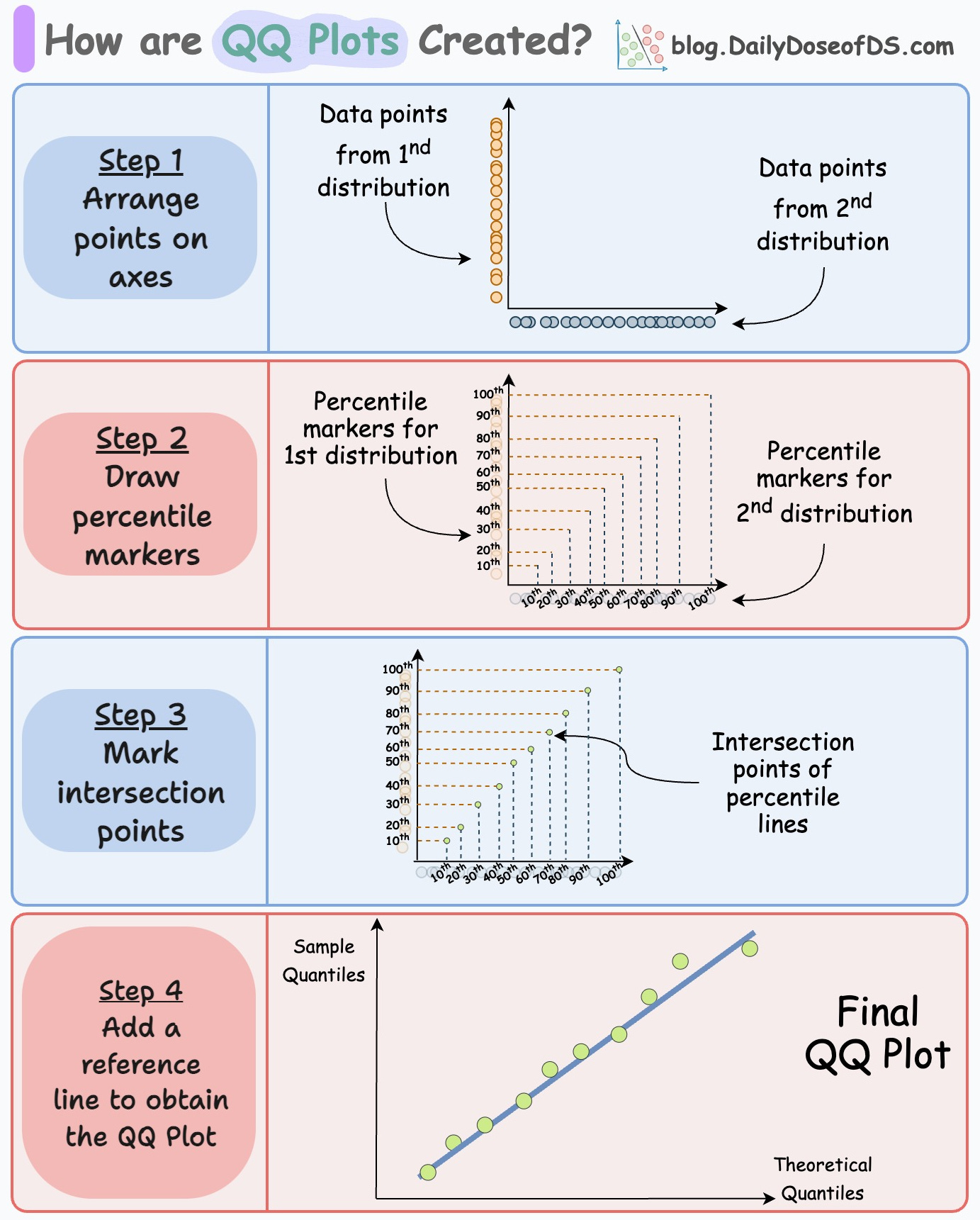
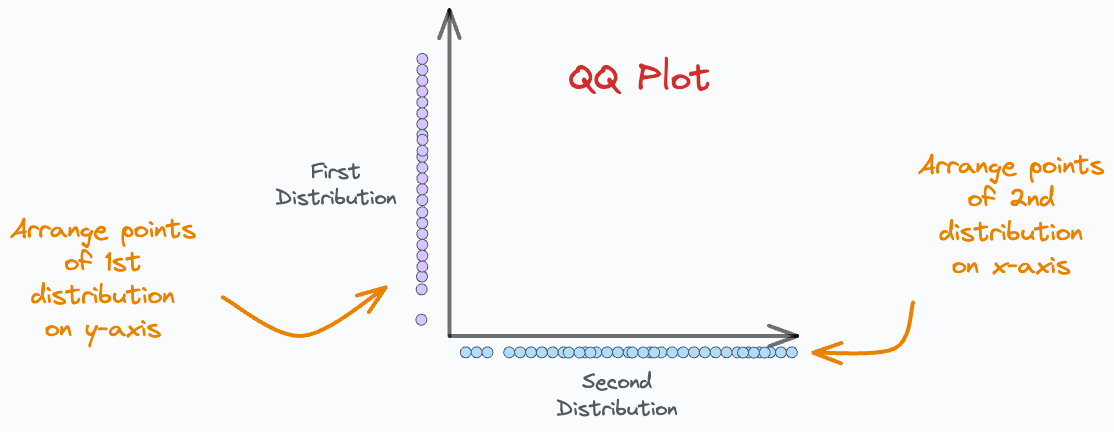
Step 1) Arrange points on axes:
As shown below, we arrange points of D1 on the y-axis and D2 on the x-axis.
Step 2) Draw percentile lines
Next, for both distributions, we create some percentile lines.
For instance, on both axes, we can mark the points of 10th percentile, 20th percentile, 30th percentile, etc., from both distributions.
This is shown below:
We mark the percentile locations for both distributions and intersect the corresponding lines.
10th percentile of D1 is intersected with 10th percentile of D2.
20th percentile of D1 is intersected with 20th percentile of D2.
and so on.
The intersection points of these percentile lines gives us the points we typically see in a QQ plot:
Now, we can get rid of the percentile marker lines.
In a gist, the above plot gives us the location where the corresponding percentiles of the two distributions match.
Step 3) Add the reference line
Finally, we must add a reference line to determine the deviations between the two distributions.
There are many ways to do this.
For instance:
The line connecting the 25th and 75th percentiles of both distributions can be considered as a reference line.
The regression fit on the above scatter plot can be considered as a reference line.
Typically, the line connecting the 25-75th percentile is preferred because the regression fit can be influenced by outliers.
After adding the reference line, we get our QQ plot:
The deviations from this reference line indicate that the two distributions differ from each other.
In other words, the deviations mean that the corresponding percentiles do not align.
This becomes an indicator of distributional dissimilarities.
And, of course, the more percentiles we plot, the better and more accurate the QQ plot will be.
There are many applications of the QQ plot.
For instance, say we have an observed distribution and want to determine if it resembles a normal distribution.
We can use a QQ plot for this:
D1: The observed distribution
D2: Normal distribution.
If the percentile points lie closer to the reference line, this would mean that the observed distribution is more like a normal distribution. This is depicted below:
👉 Over to you: What other plots do you typically struggle with and want me to cover?
Thanks for reading!
Are you preparing for ML/DS interviews or want to upskill at your current job?
Every week, I publish in-depth ML dives. The topics align with the practical skills that typical ML/DS roles demand.
Join below to unlock all full articles:
Here are some of the top articles:
[FREE] A Beginner-friendly and Comprehensive Deep Dive on Vector Databases.
8 Fatal (Yet Non-obvious) Pitfalls and Cautionary Measures in Data Science.
5 Must-Know Ways to Test ML Models in Production (Implementation Included).
A Detailed and Beginner-Friendly Introduction to PyTorch Lightning: The Supercharged PyTorch
Don’t Stop at Pandas and Sklearn! Get Started with Spark DataFrames and Big Data ML using PySpark.
Federated Learning: A Critical Step Towards Privacy-Preserving Machine Learning.
You Cannot Build Large Data Projects Until You Learn Data Version Control!
Sklearn Models are Not Deployment Friendly! Supercharge Them With Tensor Computations.
Join below to unlock all full articles:
👉 If you love reading this newsletter, share it with friends!
👉 Tell the world what makes this newsletter special for you by leaving a review here :)









When two distributions A and B have the same amount of samples, would plotting their CDFs against each other produce a valid QQ plot?
Always appreciate such a straight forward explanation with visual representations, great job!