How Does a Mini-Batch Implementation of KMeans Clustering Work?

A step-by-step visual guide to mini-batch KMeans.

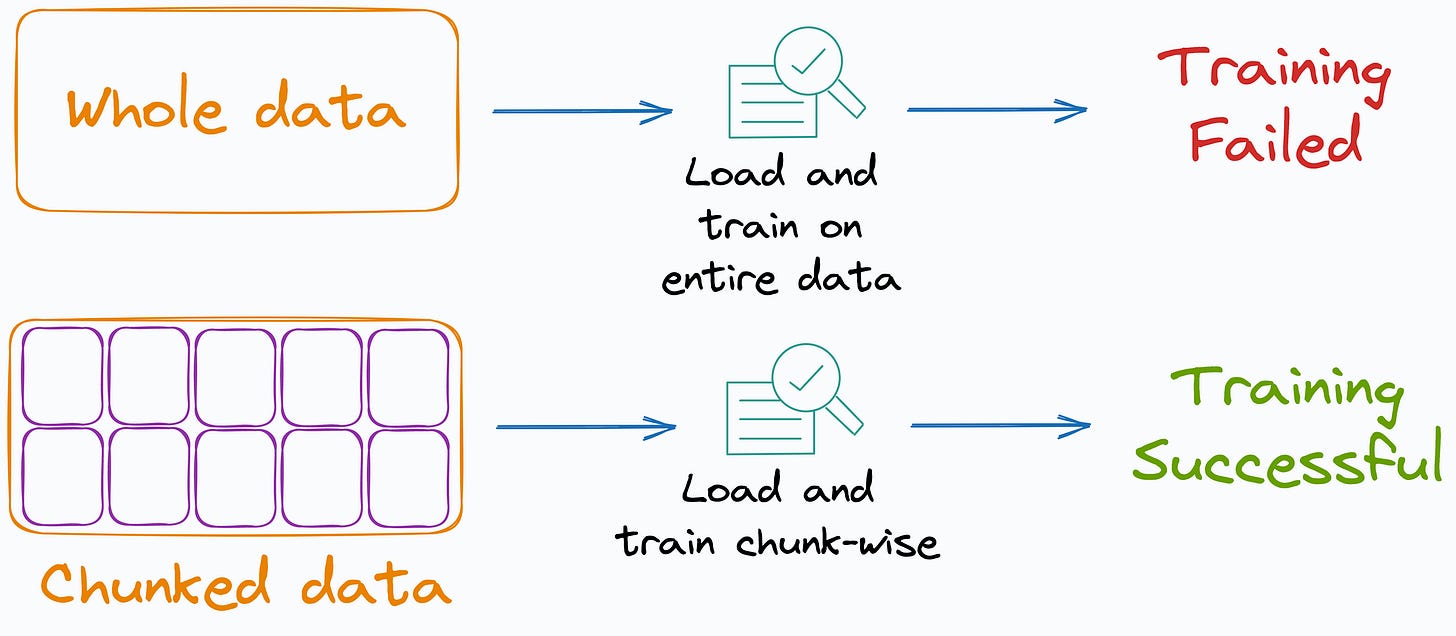
Many ML algorithms implemented by Sklearn support incremental learning, i.e., mini-batch-based training.

This makes them quite useful when the entire data does not fit into memory.

These are the supported algorithms for your reference:

If you look closely, there’s KMeans in that list too.

Being a popular clustering, it’s good that we can run it on large datasets if needed.

But when I first learned that KMeans can be implemented in a mini-batch fashion, I wondered how exactly a batch implementation of KMeans might work?

Giving it a thought for a minute or so gave me an idea, which I wish to share with you today.

Let’s begin!

---

The source of overhead in KMeans

Before understanding the mini-batch implementation, we must know the issue with the usual KMeans implementation.

To recall, KMeans works as follows:

• Step 1) Initialize centroids.

• Step 2) Find the nearest centroid for each point.

• Step 3) Reassign centroids as the average of points assigned to them.

• Step 4) Repeat until convergence.

In this implementation, the primary memory bottleneck originates from Step 3.

This is because, in this step, we compute the average of all points assigned to a centroid to shift the centroid.

Thus, traditionally, all data points assigned to a centroid must be available in memory to take an average over.

But in our case, all data points DO NOT fit into memory at once. Thus, direct averaging isn’t feasible.

Nonetheless, here’s how we can smartly address this issue.

Before I proceed further:

Honestly speaking, I haven’t checked the precise implementation of MiniBatchKMeans in Sklearn. The docs don’t tell much either.

The solution I am about to share is the one I came up with when I was trying to figure out how a mini-batch KMeans can be possibly implemented.

So if there’s a perfect overlap with Sklearn, great!

If not, it’s fine because the solution I am about to share is perfectly viable too.

---

MiniBatchKMeans

We begin the algorithm by selecting a value of k — the number of centroids.

Next, we need an initial location for the centroids so we can sample m (m << n) random data points to initialize the centroids.

Now, recall the bottleneck we discussed above — All data points must be available in memory to average over.

Thus, to address this, we need a way to keep track of the data points assigned to each centroid as we load and process each mini-batch.

We cannot maintain a growing list of data points assigned to each centroid because that would eventually take up the memory of the entire dataset.

So here’s how we can smartly fulfill this objective.

We can utilize the following mathematical property that relates sum and average:

How?

See, in a typical KMeans setting, we average over all data points assigned to a centroid to determine its new location.

But as discussed above, we can’t keep all data points in memory at once.

So how about we do this in the mini-batch setting of KMeans:

For every centroid:

• We maintain a “sum-vector”, which stores the sum of the vectors of all data points assigned to that centroid. To begin, this will be a zero vector.

• A “count” variable, which tracks the number of data points assigned to a centroid. To begin, the count will be zero.

While iterating through mini-batches:

• Every “sum-vector” of a centroid will continue to accumulate the sum of all data points that have been assigned to it so far.

• Every “count” variable of a centroid will continue to track the number of data points that have been assigned to it so far.

After iterating through all mini-batches, we can perform a scalar division between sum-vector and count to get the average vector:

This average will precisely tell us the new location of the centroid as if all data points were present in memory.

We can repeat this until convergence.

Also, before starting the next iteration of MiniBatchKMeans, we must reset the sum-vector to a zero vector and count to zero.

And that’s how a mini-batch version of KMeans can be implemented.

That was simple, wasn’t it?

---

In fact, it is quite obvious to understand that the steps we discussed above primarily involve only matrix/vector computations, which can be quickly loaded on a GPU for faster run-time.

Thus, one can easily implement a tensor implementation of KMenas.

What isn’t entirely obvious here is how you would convert, say, a decision tree or random forest to tensor computations and run it on a GPU.

If you want to learn about this, we covered it here: Sklearn Models are Not Deployment Friendly! Supercharge Them With Tensor Computations.

Also, while in this post, we talked about KMeans, it has many limitations, making it unsuitable in many situations.

Thus, being aware of other clustering algorithms and when to use them is extremely crucial.

We discussed two types of clustering algorithms → density-based and distribution-based clustering in these articles:

• DBSCAN++: The Faster and Scalable Alternative to DBSCAN Clustering

• Gaussian Mixture Models (GMMs): The Flexible Twin of KMeans.

👉 What other traditional ML algorithms do you think can be implemented in a mini-batch fashion but haven’t been implemented by Sklearn yet?

👉 If you liked this post, don’t forget to leave a like ❤️. It helps more people discover this newsletter on Substack and tells me that you appreciate reading these daily insights.

Thanks so much for appreciating the effort :)

The button is located towards the bottom of this email.

Thanks for reading!