How to Evaluate Clustering Results When You Don't Have True Labels

Three reliable methods for clustering evaluation.

Nov 19, 2023

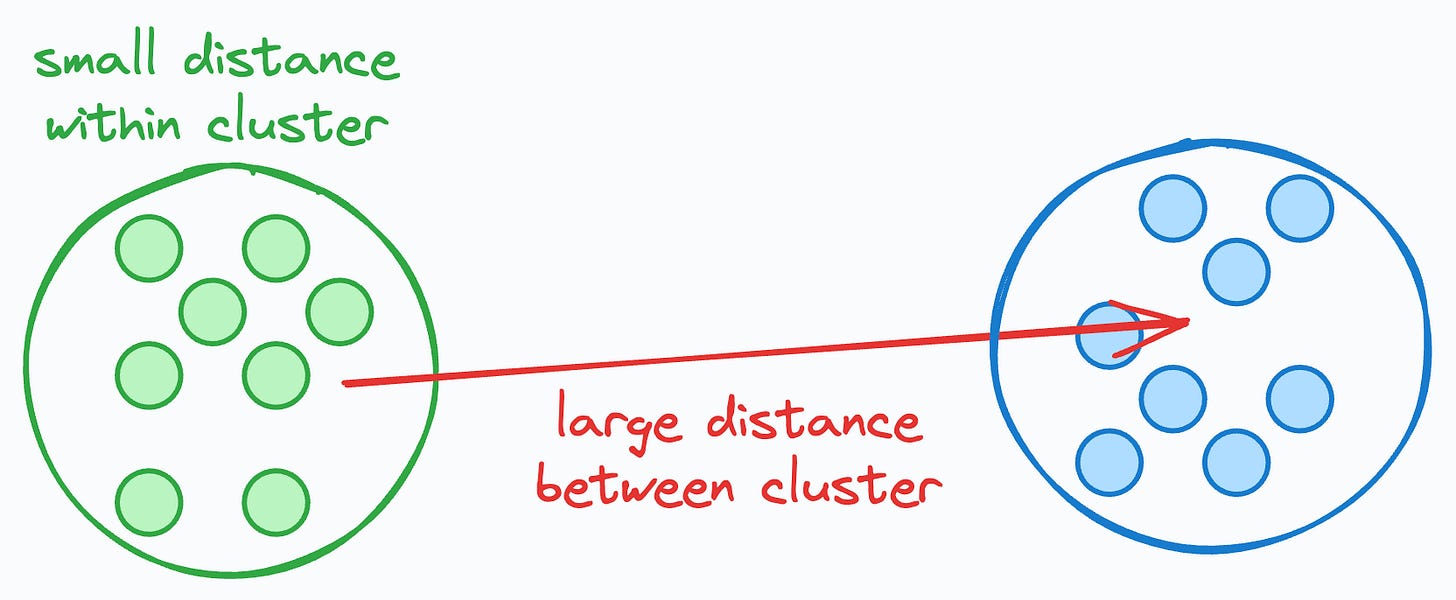
Without labeled data, it is not possible to objectively measure how well the clustering algorithm has grouped similar data points together and separated dissimilar ones.

Also, most clustering datasets are multi-dimensional, so directly visualizing the results is not possible.

Thus, we must rely on intrinsic measures to determine clustering quality in such cases.

The way I like to use them is as follows:

Say I am using KMeans:
- Run KMeans with a range of k values.
- Evaluate the performance.
- Select the value of k based on the most promising cluster quality metric.

Let’s understand a few of these metrics today.

#1) Silhouette Coefficient:

The Silhouette Coefficient indicates how well each data point fits into its assigned cluster.

The idea is that if the average distance to all data points in the same cluster is small but that to another cluster is large, this intuitively indicates that the clusters are well separated and somewhat reliable.

It is measured as follows:

For every data point:
- find the average distance to all other points within its cluster → A
- find the average distance to all points in the nearest cluster → B
- point’s score = (B-A)/max(B, A)
Compute the average of all individual scores to get the overall clustering score.

Now consider this:

If, for all data points, B is much greater than A, this would mean that:
- The average distance to points in the closest cluster is large.
- The average distance to points in the same cluster is small.
- Thus, the overall score will be close to 1, indicating that the clusters are well separated.

So, a higher Silhouette Coefficient would mean that, generally speaking, all data points fit into their ideal clusters.

Measuring it across a range of centroids (k) can reveal which clustering results are most promising:

I covered this here if you wish to understand the Silhouette Coefficient with diagrams.

#2) Calinski-Harabasz Index

Calinski-Harabasz Index is another metric that is measured quite similarly to the Silhouette Coefficient.

A → sum of squared distance between all centroids and overall dataset center.
B → sum of squared distance between all points and their specific centroid.
metric is computed as A/B (with an additional scaling factor ).

Yet again, is A is much greater than B:

The distance of centroids to the dataset center is large.
The distance of data points to their specific centroid is small
Thus, it will result in a higher score, indicating that the clusters are well separated.

The reason I prefer the Calinski-Harabasz Index over the Silhouette Coefficient is that:

It is relatively much faster to compute. Silhouette Coefficient, on the other hand, takes time when you have plenty of data points.
And it still makes the same intuitive sense for interpretation as the Silhouette Coefficient.

#3) DBCV

The issue with the Silhouette score and Calinski-Harabasz index is that they are typically higher for convex (or somewhat spherical) clusters.

However, using them to evaluate arbitrary-shaped clustering, like those obtained with density-based clustering, can produce misleading results.

This is evident from the image below:

As depicted above, while the clustering output of KMeans is worse, the Silhouette score is still higher than Density-based clustering.

DBCV — density-based clustering validation is a better metric in such cases.

As the name suggests, it is specifically meant to evaluate density-based clustering.

Simply put, DBCV computes two values:

The density within a cluster
The density overlap between clusters

A high density within a cluster and a low density overlap between clusters indicate good clustering results.

The effectiveness of DBCV is also evident from the image below:

With DBCV, the score for the clustering output of KMeans is worse, and that of density-based clustering is higher.

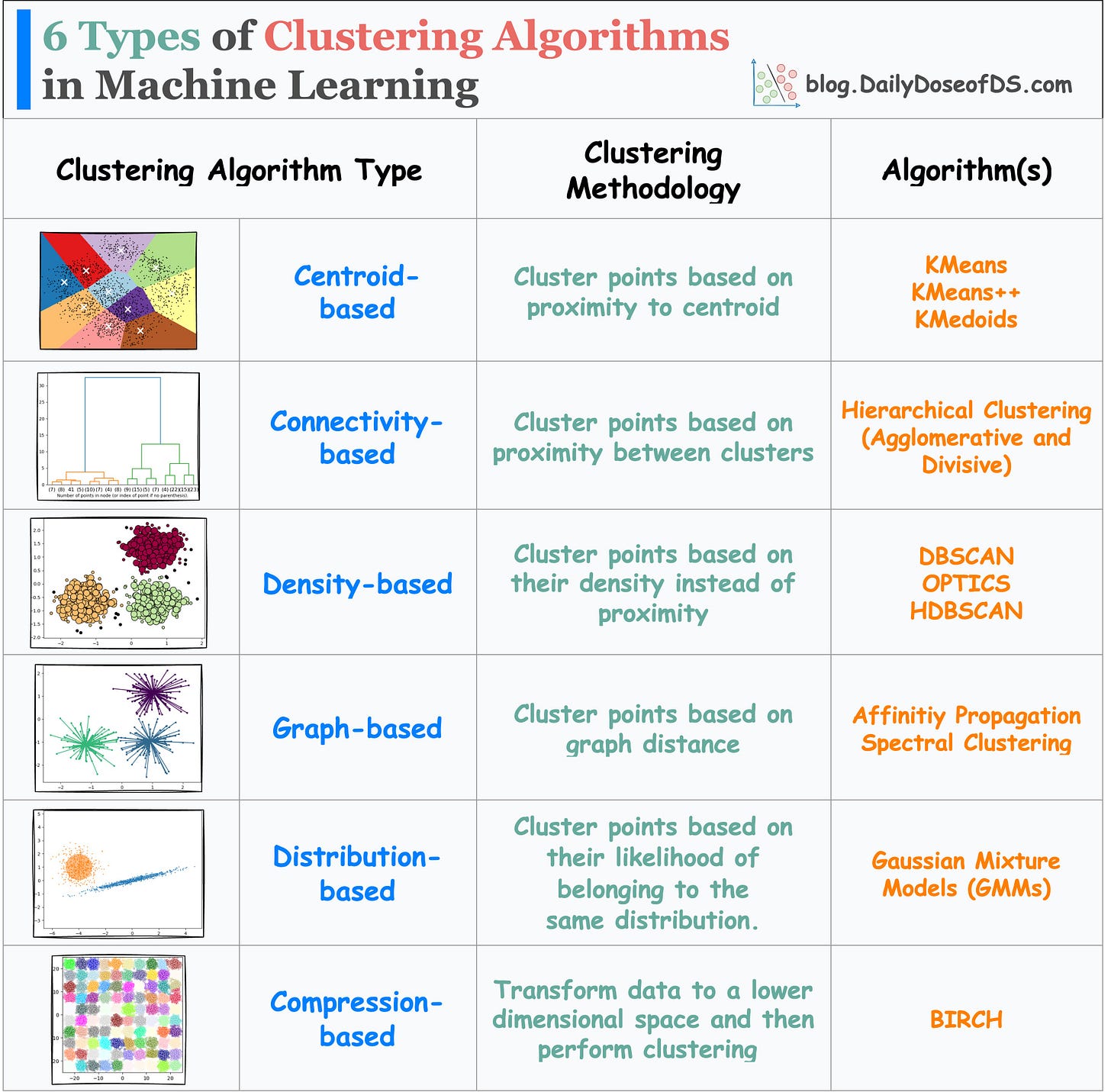
Before I conclude, do note that there are other types of clustering algorithms too, as depicted in the visual below:

In this post, we covered centroid-based and density-based evaluation. You can read about Distributed-based clustering and its evaluation here: Gaussian Mixture Models (GMMs).

👉 Over to you: What are some other ways to evaluate clustering performance in such situations?

👉 If you liked this post, don’t forget to leave a like ❤️. It helps more people discover this newsletter on Substack and tells me that you appreciate reading these daily insights.