How to Find Optimal Epsilon Value For DBSCAN Clustering?
Using Elbow Curve outside KMeans.
In DBSCAN, determining the epsilon parameter is often tricky.
Yet, the Elbow curve is often helpful in determining it.
To begin, DBSCAN has three hyperparameters:
Epsilon: two points are considered neighbors if they are closer than Epsilon.
min_samples: Min neighbors for a point to be classified as a core point.
The distance metric.
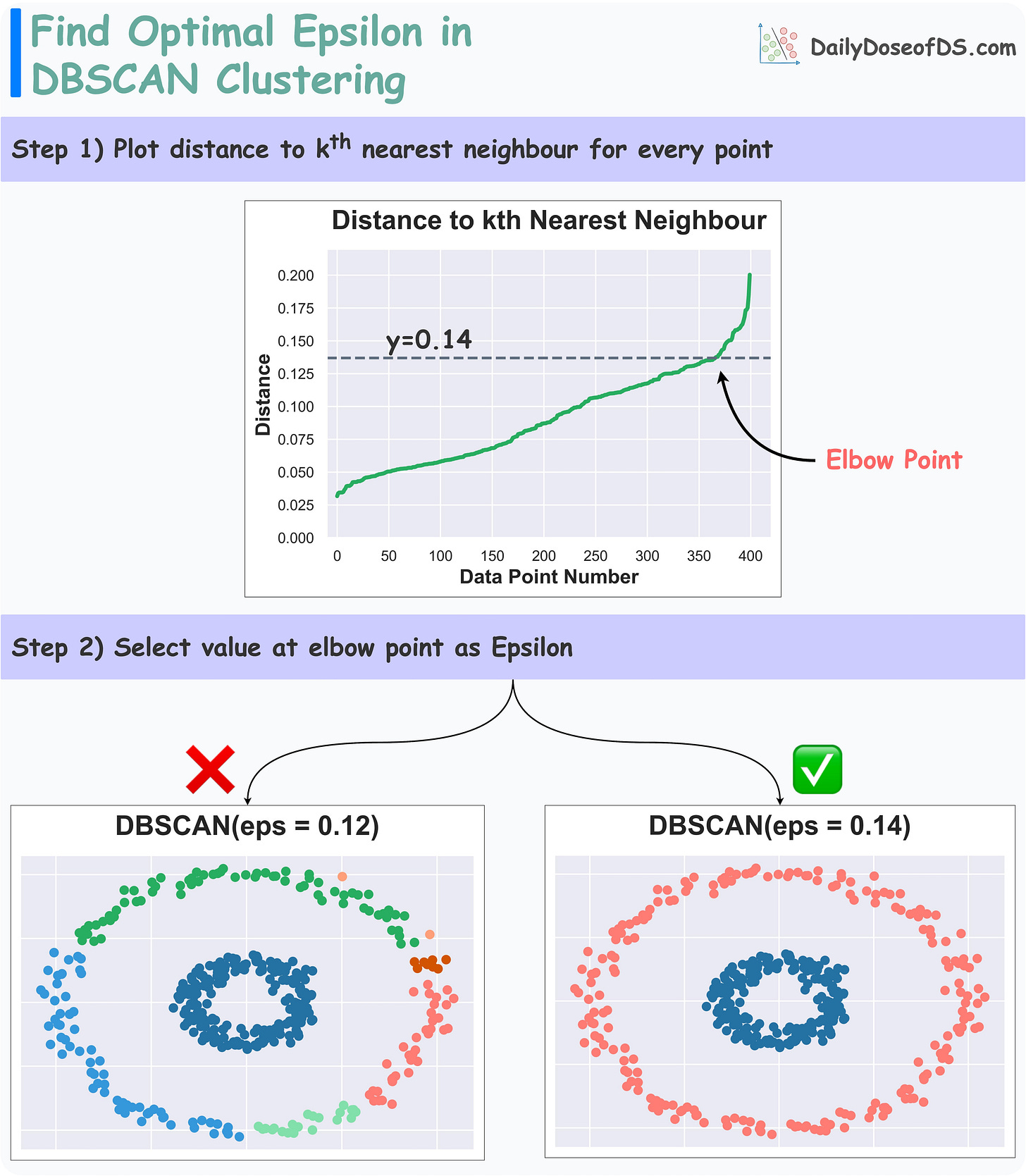
We can use the Elbow Curve to find an optimal value of Epsilon:
Set k as the min_samples hyperparameter.
For every data point, plot the distance to its kth nearest neighbor (in increasing order).
The optimal value of Epsilon is found near the elbow point.
Why does it work?
Recall that we are measuring the distance to a specific (kth) neighbor for all points.
Thus, the elbow point suggests a distance to a more isolated point or a point in a different cluster.
The point where change is most pronounced hints towards an optimal epsilon.
The efficacy is evident from the image above.
Selecting the elbow value provides better clustering results over another value.
👉 Over to you: What methods do you use to find an optimal epsilon for DBSCAN?
Thanks for reading!
Hey there!
The next member-only post will be released tomorrow.
Only a few hours remain before the subscription offer ends.
By subscribing before tomorrow:
Any pricing updates will NEVER affect your plan.
Pause and renew anytime at the same price.
Upcoming courses and bonus resources (practice notebooks, extensive study guides, etc.) will be included.
Thanks :)
👉 Tell the world what makes this newsletter special for you by leaving a review here :)
👉 If you love reading this newsletter, feel free to share it with friends!
👉 Sponsor the Daily Dose of Data Science Newsletter. More info here: Sponsorship details.
I like to explore, experiment and write about data science concepts and tools. You can connect with me on LinkedIn and Twitter.