KernelPCA vs. PCA for Dimensionality Reduction
...and when to not use KernelPCA.
During dimensionality reduction, principal component analysis (PCA) tries to find a low-dimensional linear subspace that the given data conforms to.
For instance, consider the following dummy dataset:
It’s pretty clear from the above visual that there is a linear subspace along which the data could be represented while retaining maximum data variance. This is shown below:
But what if our data conforms to a low-dimensional yet non-linear subspace.
For instance, consider the following dataset:
Do you see a low-dimensional non-linear subspace along which our data could be represented?
No?
Don’t worry. Let me show you!
The above curve is a continuous non-linear and low-dimensional subspace that we could represent our data given along.
Okay…so why don’t we do it then?
The problem is that PCA cannot determine this subspace because the data points are non-aligned along a straight line.
In other words, PCA is a linear dimensionality reduction technique.
Thus, it falls short in such situations.
Nonetheless, if we consider the above non-linear data, don’t you think there’s still some intuition telling us that this dataset can be reduced to one dimension if we can capture this non-linear curve.
KernelPCA (or the kernel trick) precisely addresses this limitation of PCA.
The idea is pretty simple.
In standard PCA, we compute the eigenvectors and eigenvalues of the standard covariance matrix (we covered the mathematics here).
In KernelPCA, however:
We first use a kernel function to compute the pairwise high-dimensional dot product between two data points, X and Y, without explicitly projecting the vectors to that space.
This produces a kernel matrix.
Next, perform eigendecomposition on this kernel matrix instead and select the top “
p” components.Done!
If there's any confusion in the above steps, I would highly recommend reading this deep dive on PCA, where we formulated the entire PCA algorithm from scratch. It will help you understand the underlying mathematics.
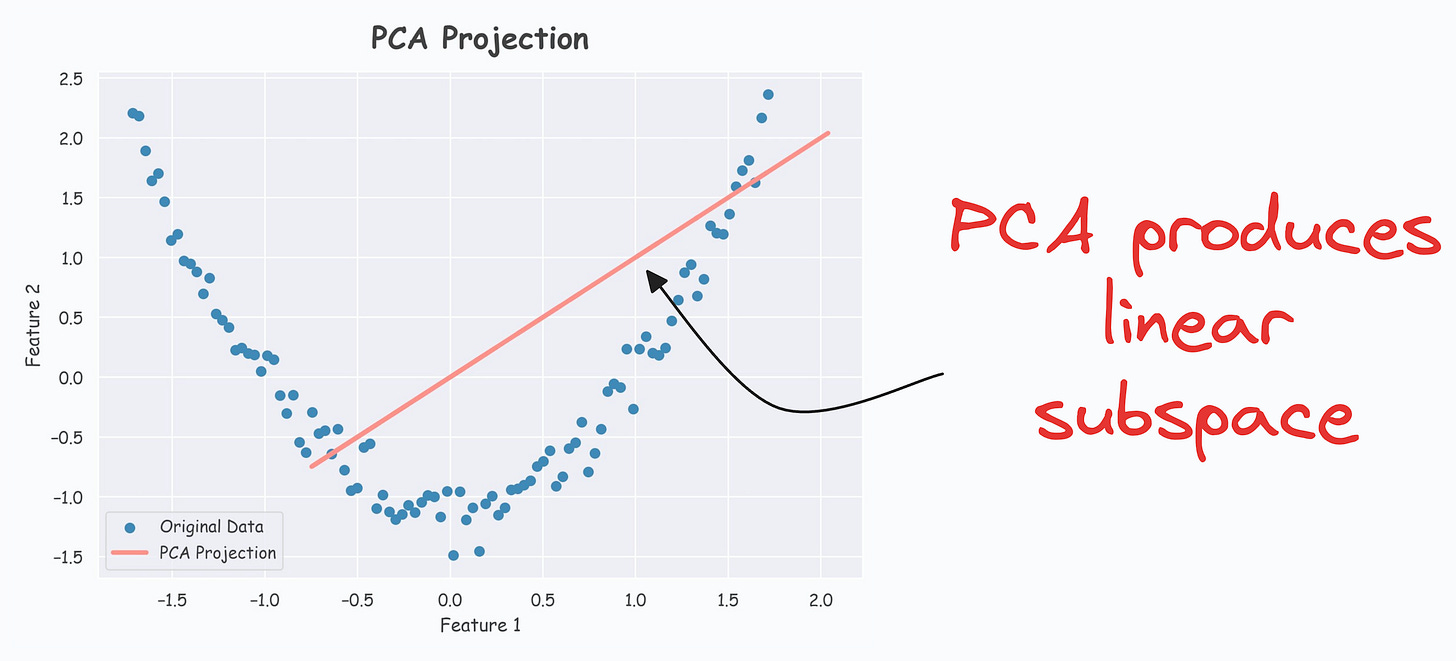
The efficacy of KernelPCA over PCA is evident from the demo below.
As shown below, even though the data is non-linear, PCA still produces a linear subspace for projection:
However, KernelPCA produces a non-linear subspace:
That’s handy, isn’t it?
What’s the catch?
The catch here is the run time.
Since we compute the pairwise dot products in KernelPCA, this adds an additional O(n^2) time-complexity.
Thus, it increases the overall run time. This is something to be aware of when using KernelPCA.
If you want to dive into the clever mathematics of the kernel trick and why it is called a “trick,” we covered this in the newsletter here:
👉 Over to you: What are some other limitations of PCA?
P.S. For those wanting to develop “Industry ML” expertise:
At the end of the day, all businesses care about impact. That’s it!
Can you reduce costs?
Drive revenue?
Can you scale ML models?
Predict trends before they happen?
We have discussed several other topics (with implementations) in the past that align with such topics.
Here are some of them:
Learn sophisticated graph architectures and how to train them on graph data: A Crash Course on Graph Neural Networks – Part 1.
So many real-world NLP systems rely on pairwise context scoring. Learn scalable approaches here: Bi-encoders and Cross-encoders for Sentence Pair Similarity Scoring – Part 1.
Learn techniques to run large models on small devices: Quantization: Optimize ML Models to Run Them on Tiny Hardware.
Learn how to generate prediction intervals or sets with strong statistical guarantees for increasing trust: Conformal Predictions: Build Confidence in Your ML Model’s Predictions.
Learn how to identify causal relationships and answer business questions: A Crash Course on Causality – Part 1
Learn how to scale ML model training: A Practical Guide to Scaling ML Model Training.
Learn techniques to reliably roll out new models in production: 5 Must-Know Ways to Test ML Models in Production (Implementation Included)
Learn how to build privacy-first ML systems: Federated Learning: A Critical Step Towards Privacy-Preserving Machine Learning.
Learn how to compress ML models and reduce costs: Model Compression: A Critical Step Towards Efficient Machine Learning.
All these resources will help you cultivate key skills that businesses and companies care about the most.