Logistic Regression Can NEVER Perfectly Model Well-separated Classes

But isn't well-separated data easiest to separate?

Recently, I was experimenting with a logistic regression model in one of my projects.

While understanding its convergence using the epoch-by-epoch loss value, I discovered something peculiar about logistic regression that I had never realized before:

Logistic regression can never perfectly model well-separated classes.

Confused?

Let me explain my thought process.

For simplicity, we shall be considering a dataset with just one feature X.

---

Background

We all know that logistic regression outputs the probability of a class, which is given by:

What’s more, its loss function is the binary cross-entropy loss (or log loss), which is written as:

yᵢ is the true label, and ŷᵢ is the predicted probability

• When the true label yᵢ = 1, the loss value is → -log(ŷᵢ).

• When the true label yᵢ = 0, the loss value is → -log(1-ŷᵢ).

And as we all know, the model attempts to determine the parameters (θ₀, θ₁) by minimizing the loss function.

Proof

The above output probability can be rewritten as follows:

Simply put, we have represented the output probability function in terms of two other parameters.

All good?

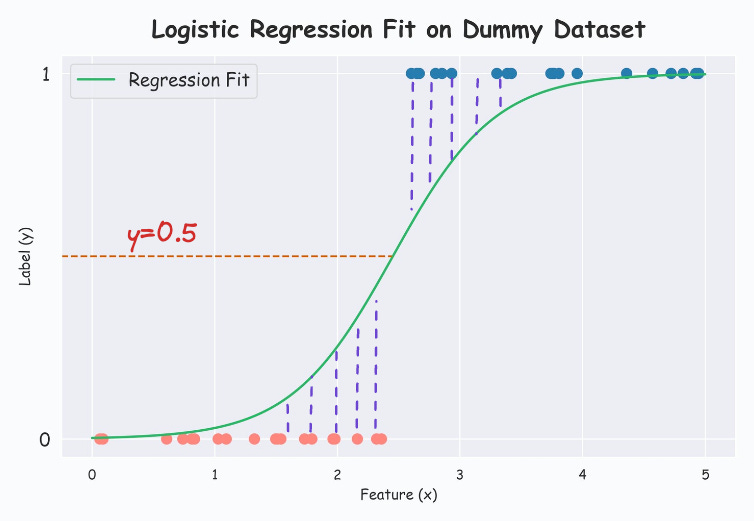
Now consider the following 1D dataset with well-separated classes:

Modeling this with a logistic regression model from sklearn, we get the following:

Printing the (m,c) values from the below formulation, we get m=2.21, c=-2.33.

Let’s see if we can obtain a better regression curve now.

More specifically, we shall try fitting a logistic regression model with different different values of m.

The results are shown below:

From the above visual, it is clear that increasing the m parameter consistently leads to:

• A smaller (yet non-zero) loss value.

• A better regression fit.

And to obtain the best regression fit, the sigmoid curve must be entirely vertical in the middle, which is never possible.

Thus, the abovementioned point: “Logistic regression can never perfectly fit well-separated classes” is entirely valid.

That is why many open-source implementations (sklearn, for instance) stop after a few iterations.

So it is important to note that they still leave a little scope for improvement if needed.

I would love to know your thoughts on this little experiment.

---

On a side note, have you ever wondered the following:

1. Why do we use Sigmoid in logistic regression?

2. Why do we ‘log loss’ in logistic regression?

Why not any other functions?

They can’t just appear from thin air, can they? There must be some mathematically-backed origin, no?

Check out these two deep dives to learn this:

• Why Do We Use Sigmoid in Logistic Regression?

• Why Do We Use ‘log loss’ to Train Logistic Regression?

---

👉 If you liked this post, don’t forget to leave a like ❤️. It helps more people discover this newsletter on Substack and tells me that you appreciate reading these daily insights.

Thanks so much for appreciating the effort :)

The button is located towards the bottom of this email.

Thanks for reading!

---

Latest full articles

If you’re not a full subscriber, here’s what you missed:

• DBSCAN++: The Faster and Scalable Alternative to DBSCAN Clustering

• Federated Learning: A Critical Step Towards Privacy-Preserving Machine Learning

• You Cannot Build Large Data Projects Until You Learn Data Version Control!

• Why Bagging is So Ridiculously Effective At Variance Reduction?

• Sklearn Models are Not Deployment Friendly! Supercharge Them With Tensor Computations.

• Deploy, Version Control, and Manage ML Models Right From Your Jupyter Notebook with Modelbit

• Gaussian Mixture Models (GMMs): The Flexible Twin of KMeans.

• Bayesian Optimization for Hyperparameter Tuning.

To receive all full articles and support the Daily Dose of Data Science, consider subscribing:

---

👉 Tell the world what makes this newsletter special for you by leaving a review here :)

👉 If you love reading this newsletter, feel free to share it with friends!