Logistic Regression Cannot Perfectly Model Well-separated Classes
But isn't well-separated data easiest to separate?
I have made several observations when using logistic regression, but one of them is a bit peculiar:
Logistic regression can never perfectly model well-separated classes.
Confused?
Let me explain my thought process.
For simplicity, we shall be considering a dataset with just one feature X.
Background
We all know that logistic regression outputs the probability of a class, which is given by:
What’s more, its loss function is the binary cross-entropy loss (or log loss), which is written as:
When the true label yᵢ = 1, the loss value is → -log(ŷᵢ).
When the true label yᵢ = 0, the loss value is → -log(1-ŷᵢ).
And as we all know, the model attempts to determine the parameters (θ₀, θ₁) by minimizing the loss function.
Proof
The above output probability can be rewritten as follows:
Simply put, we have represented the output probability function in terms of two other parameters.
All good?
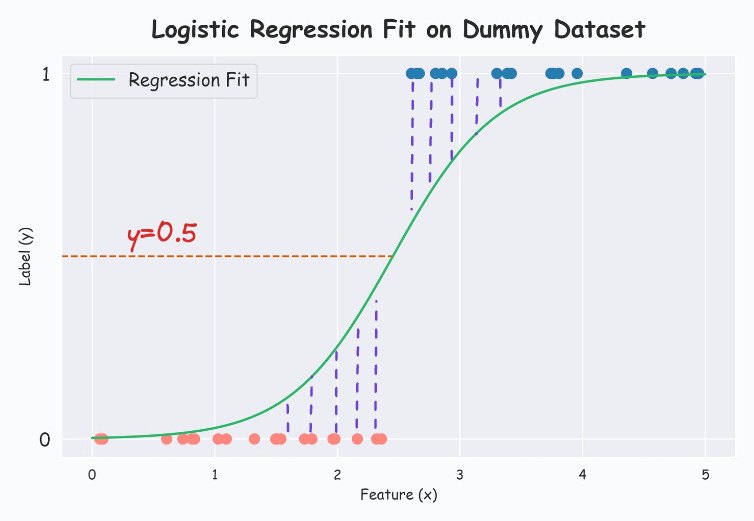
Now consider the following 1D dataset with well-separated classes:
Modeling this with a logistic regression model from sklearn, we get the following:
Printing the (m,c) values from the below formulation, we get m=2.21, c=-2.33.
Let’s see if we can obtain a better regression curve now.
More specifically, we shall try fitting a logistic regression model with different different values of m.
The results are shown below:
From the above visual, it is clear that increasing the m parameter consistently leads to:
A smaller (yet non-zero) loss value.
A better regression fit.
And to obtain the best regression fit, the sigmoid curve must be entirely vertical in the middle, which is never possible.
Thus, the abovementioned point: “Logistic regression can never perfectly fit well-separated classes” is entirely valid.
That is why many open-source implementations (sklearn, for instance) stop after a few iterations.
So it is important to note that they still leave a little scope for improvement if needed.
I would love to know your thoughts on this little experiment.
On a side note, have you ever wondered the following:
Why do we use Sigmoid in logistic regression?
Why do we ‘log loss’ in logistic regression?
Why sklearn’s logistic regression has no learning rate hyperparamter?
Check out these two deep dives to learn this:
Are you overwhelmed with the amount of information in ML/DS?
Every week, I publish no-fluff deep dives on topics that truly matter to your skills for ML/DS roles.
For instance:
Quantization: Optimize ML Models to Run Them on Tiny Hardware
A Beginner-friendly Introduction to Kolmogorov Arnold Networks (KANs)
5 Must-Know Ways to Test ML Models in Production (Implementation Included)
Understanding LoRA-derived Techniques for Optimal LLM Fine-tuning
8 Fatal (Yet Non-obvious) Pitfalls and Cautionary Measures in Data Science
Implementing Parallelized CUDA Programs From Scratch Using CUDA Programming
You Are Probably Building Inconsistent Classification Models Without Even Realizing
And many many more.
Join below to unlock all full articles:
SPONSOR US
Get your product in front of 82,000 data scientists and other tech professionals.
Our newsletter puts your products and services directly in front of an audience that matters — thousands of leaders, senior data scientists, machine learning engineers, data analysts, etc., who have influence over significant tech decisions and big purchases.
To ensure your product reaches this influential audience, reserve your space here or reply to this email to ensure your product reaches this influential audience.