Most People Don’t Entirely Understand How Dropout Works
Here's the remaining information which you must know.
A couple of weeks back, I was invited by a tech startup to conduct their ML interviews.
I interviewed 12 candidates and mostly asked practical ML questions.
However, there were some conceptual questions as well, like the one below, which I intentionally asked every candidate:
How does Dropout work?
Pretty simple, right?
Apparently, every candidate gave me an incomplete answer, which I have mentioned below:
Candidates’ Answer
In a gist, the idea is to zero out neurons randomly in a neural network. This is done to regularize the network.
Dropout is only applied during training, and which neuron activations to zero out (or drop) is decided using a Bernoulli distribution:
My follow-up question: Okay, perfect! Is there anything else that we do in Dropout?
Candidates: No, that’s it. We only zero out neurons and train the network as we usually would.
Now, coming back to this newsletter issue…
Of course, I am not saying that the above details are incorrect.
They are correct.
However, this is just 50% of how Dropout works, and disappointingly, most resources don’t cover the remaining 50%.
If you too, are only aware of the 50% details I mentioned above, then continue reading as there’s new information for you.
How Dropout actually works?
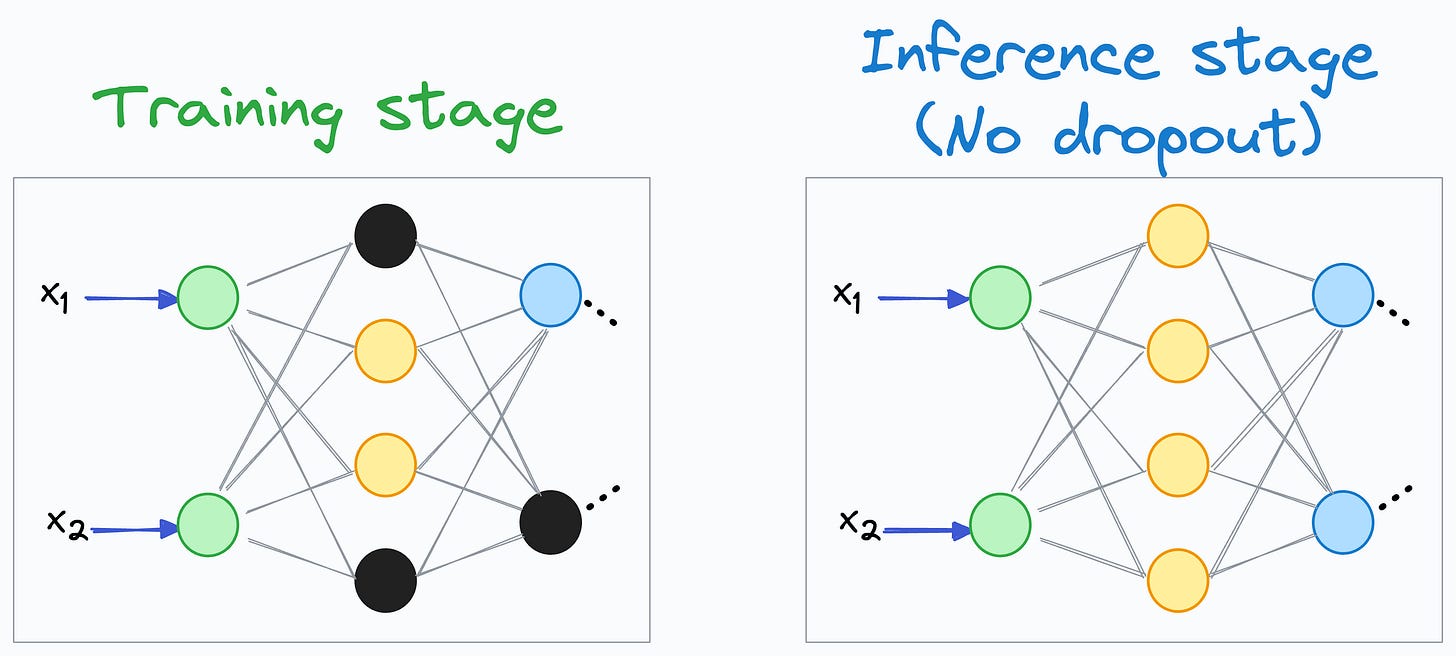
To begin, we must note that Dropout is only applied during training, but not during the inference/evaluation stage:
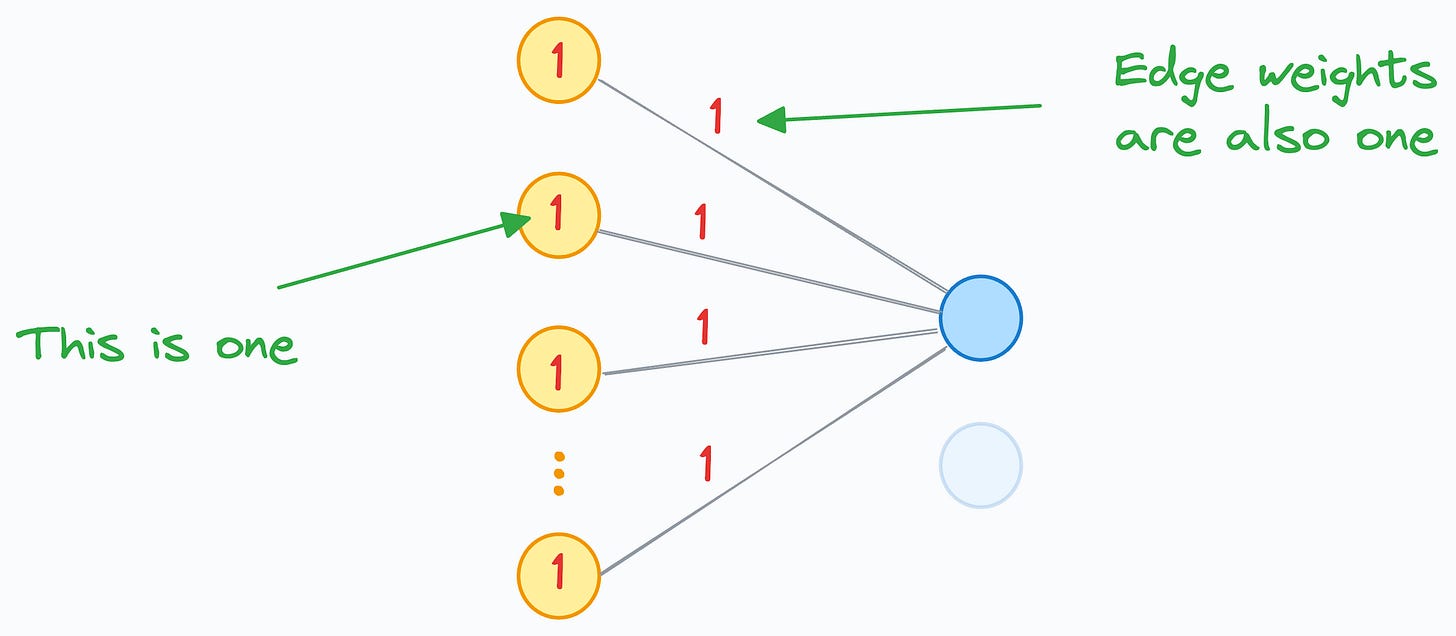
Now, consider that a neuron’s input is computed using 100 neurons in the previous hidden layer:
For simplicity, let’s assume a couple of things here:
The activation of every yellow neuron is 1.
The edge weight from the yellow neurons to the blue neuron is also 1.
As a result, the input received by the blue neuron will be 100, as depicted below:
All good?
Now, during training, if we were using Dropout with, say, a 40% dropout rate, then roughly 40% of the yellow neuron activations would have been zeroed out.
As a result, the input received by the blue neuron would have been around 60, as depicted below:
However, the above point is only valid for the training stage.
If the same scenario had existed during the inference stage instead, then the input received by the blue neuron would have been 100.
Thus, under similar conditions:
The input received during training → 60.
The input received during inference → 100.
Do you see any problem here?
During training, the average neuron inputs are significantly lower than those received during inference.
More formally, using Dropout significantly affects the scale of the activations.
However, it is desired that the neurons throughout the model must receive the roughly same mean (or expected value) of activations during training and inference.
To address this, Dropout performs one additional step.
This idea is to scale the remaining active inputs during training.
The simplest way to do this is by scaling all activations during training by a factor of 1/(1-p), where p is the dropout rate.
For instance, using this technique on the neuron input of 60, we get the following (recall that we set p=40%):
As depicted above, scaling the neuron input brings it to the desired range, which makes training and inference stages coherent for the network.
Verifying experimentally
In fact, we can verify that typical implementations of Dropout, from PyTorch, for instance, do carry out this step.
Let’s define a dropout layer as follows:
Now, let’s consider a random tensor and apply this dropout layer to it:
As depicted above, the retained values have increased.
The second value goes from 0.13 → 0.16.
The third value goes from 0.93 → 1.16.
and so on…
What’s more, the retained values are precisely the same as we would have obtained by explicitly scaling the input tensor with 1/(1-p):
If we were to do the same thing in evaluation mode instead, we notice that no value is dropped and no scaling takes place either, which makes sense as Dropout is only used during training:
This is the remaining 50% details, which, in my experience, most resources do not cover, and as a result, most people aren’t aware of.
But it is a highly important step in Dropout, which maintains numerical coherence between training and inference stages.
With that, now you know 100% of how Dropout works.
👉 Over to you: What are some other ways to regularize neural networks?
👉 If you liked this post, don’t forget to leave a like ❤️. It helps more people discover this newsletter on Substack and tells me that you appreciate reading these daily insights.
The button is located towards the bottom of this email.
Thanks for reading!
Latest full articles
If you’re not a full subscriber, here’s what you missed last month:
How To (Immensely) Optimize Your Machine Learning Development and Operations with MLflow.
Don’t Stop at Pandas and Sklearn! Get Started with Spark DataFrames and Big Data ML using PySpark.
DBSCAN++: The Faster and Scalable Alternative to DBSCAN Clustering.
Federated Learning: A Critical Step Towards Privacy-Preserving Machine Learning.
You Cannot Build Large Data Projects Until You Learn Data Version Control!
Deploy, Version Control, and Manage ML Models Right From Your Jupyter Notebook with Modelbit.
To receive all full articles and support the Daily Dose of Data Science, consider subscribing:
👉 Tell the world what makes this newsletter special for you by leaving a review here :)
👉 If you love reading this newsletter, feel free to share it with friends!














There are two ways it can be handled. The paper on dropout says that during inference they multiply the probability of dropout with the activations of that layers. Where as the implementation in the library such as PyTorch and other, the compensation is done during the training by scaling the activations. Great write up. So true that many doesn’t the scaling factors and many senior people who read the paper says only inference way of compensation is correct.
Avi TBH, it would be very interesting if you'd create a blog post listing the practical ML questions (with answers) you've asked the candidates during the interview!