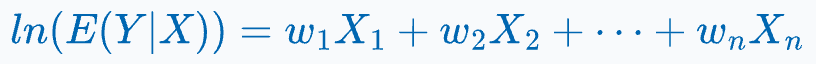Poisson Regression vs. Linear Regression
Linear regression is not the only linear model.
Today, we shall understand Poisson regression, a type of generalized linear model (GLM), and we covered 4 types of GLMs in detail here: Generalized Linear Models (GLMs): The Supercharged Linear Regression.
Let’s begin!
Linear regression comes with its own set of challenges/assumptions.
For instance, after modeling, the output can be negative for some inputs.
But this may not make sense at times — predicting the number of goals scored, number of calls received, etc.
Thus, it is clear that it cannot model count (or discrete) data.
Furthermore, in linear regression:
Residuals are expected to be normally distributed around the mean.
Hence, the outcomes on either side of the mean (m-x, m+x) are equally likely.
For instance:
if the expected number (mean) of calls received is 1...
...then, according to linear regression, receiving 3 calls (1+2) is just as likely as receiving -1 (1-2) calls. (This relates to the concept of prediction intervals, which I will cover in an upcoming issue.)
But in this case, a negative prediction does not make any sense.
Thus, if the above assumptions do not hold, linear regression won’t help.
Instead, in this specific case, what you may need is Poisson regression.
Poisson regression:
is more suitable if your response (or outcome) is count-based.
assumes that the response comes from a Poisson distribution.
It is a type of generalized linear model (GLM) that is used to model count data.
It works by estimating a Poisson distribution parameter (λ), which is directly linked to the expected number of events in a given interval.
Contrary to linear regression, in Poisson regression:
Residuals may follow an asymmetric distribution around the mean (λ).
Hence, outcomes on either side of the mean (λ-x, λ+x) are NOT equally likely.
For instance:
if the expected number (mean) of calls received is 1...
...then, according to Poisson regression, it is possible to receive 3 (1+2) calls, but it is impossible to receive -1 (1-2) calls.
This is because its outcome is also non-negative.
The regression fit is mathematically defined as follows:
The effectiveness of Poisson regression is evident from the image below:
The following visual neatly summarizes this post:
While this was just about Poisson regression — one of the many members of the generalized linear models (GLMs) family, here’s a deep dive to learn everything about GLMs: Generalized Linear Models (GLMs): The Supercharged Linear Regression.
👉 Over to you: Can you tell me some limitations or considerations for using Poisson regression?
Are you overwhelmed with the amount of information in ML/DS?
Every week, I publish no-fluff deep dives on topics that truly matter to your skills for ML/DS roles.
For instance:
A Beginner-friendly Introduction to Kolmogorov Arnold Networks (KANs).
5 Must-Know Ways to Test ML Models in Production (Implementation Included).
Understanding LoRA-derived Techniques for Optimal LLM Fine-tuning
8 Fatal (Yet Non-obvious) Pitfalls and Cautionary Measures in Data Science
Implementing Parallelized CUDA Programs From Scratch Using CUDA Programming
You Are Probably Building Inconsistent Classification Models Without Even Realizing.
And many many more.
Join below to unlock all full articles:
SPONSOR US
Get your product in front of 80,000 data scientists and other tech professionals.
Our newsletter puts your products and services directly in front of an audience that matters — thousands of leaders, senior data scientists, machine learning engineers, data analysts, etc., who have influence over significant tech decisions and big purchases.
To ensure your product reaches this influential audience, reserve your space here or reply to this email to ensure your product reaches this influential audience.