Statsmodel Regression Summary Will Never Intimidate You Again
The statsmodel summary guide you always wanted to read.
Statsmodel provides one of the most comprehensive summaries for regression analysis.
Yet, I have seen so many people struggling to interpret the critical model details mentioned in this report.
Today, let me help you understand the entire summary support provided by statsmodel and why it is so important.
Let’s begin!
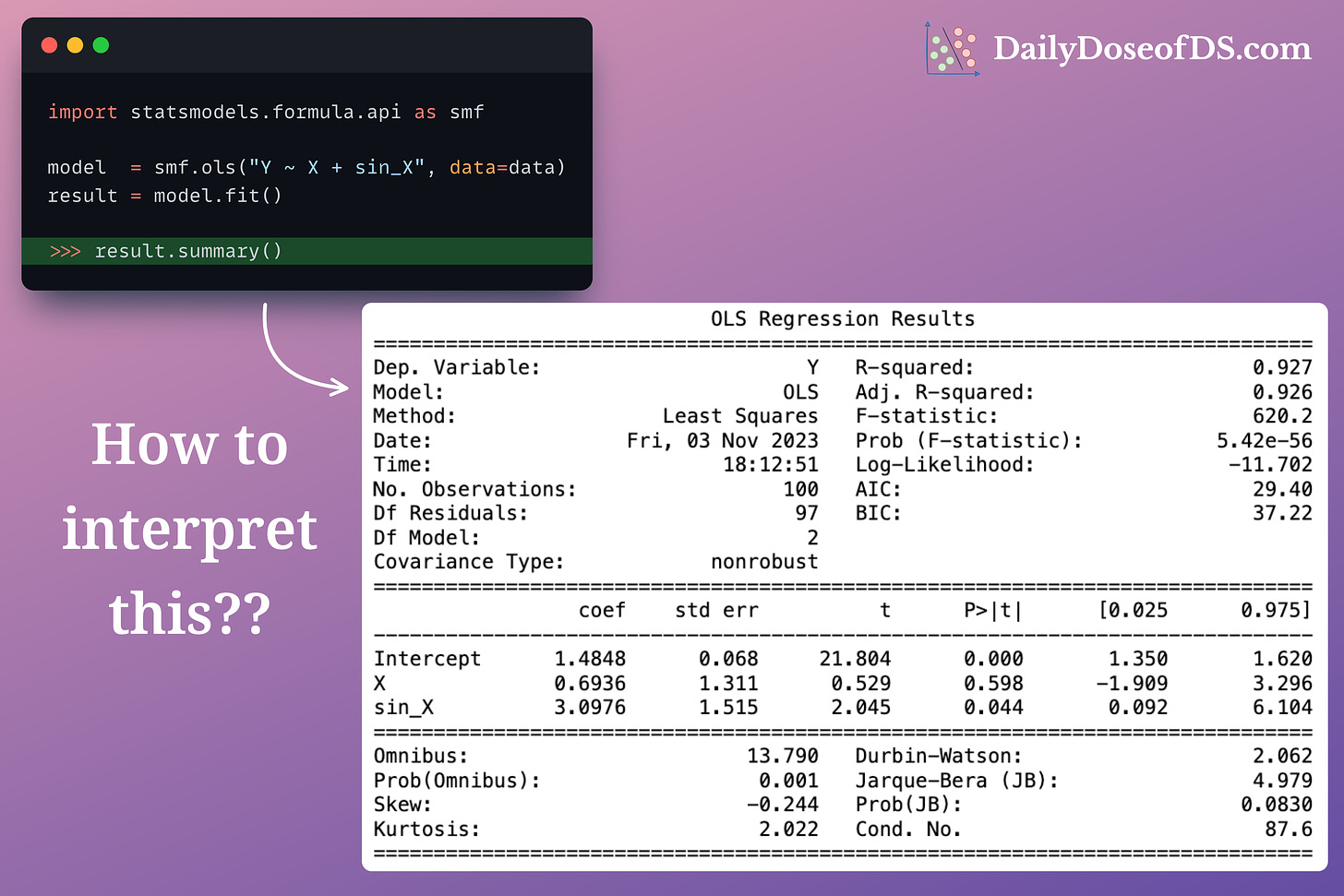
The first column of the first section lists the model’s settings (or config). This part has nothing to do with the model’s performance.
Dependent variable: The variable we are predicting.
Model and Method: We are using OLS to fit a linear model.
Date and time: You know it.
No. of observations: The dataset’s size.
Df residuals: The degrees of freedom associated with the residuals. It is essentially the number of data points minus the number of parameters estimated in the model (including intercept term).
Df Model: This represents the degrees of freedom associated with the model. It is the number of predictors, 2 in our case —
Xandsin_X.
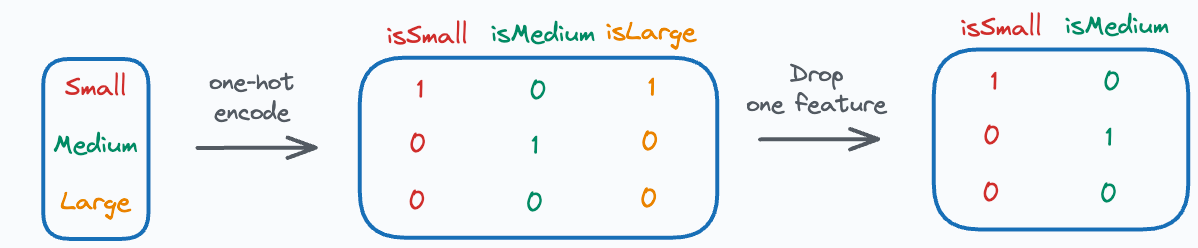
If your data has categorical features, statsmodel will one-hot encode them. But in that process, it will drop one of the one-hot encoded features.
This is called the dummy variable trap, which we discussed in this newsletter here.
Covariance type: This is related to the assumptions about the distribution of the residual.
In linear regression, we assume that the residuals have a constant variance (homoscedasticity). Why? We discussed it here.
We use “nonrobust” to train a model under that assumption.
In the second column, statsmodel provides the overall performance-related details:
R-squared: The fraction of original data variability captured by the model.
For instance, in this case, 0.927 means that the current model captures 92.7% of the original variability in the training data.
Statsmodel reports R2 on the input data, so you must not overly optimize for it. If you do, it will lead to overfitting.
Adj. R-squared:
It is somewhat similar to R-squared, but it also accounts for the number of predictors (features) in the model.
The problem is that R-squared always increases as we add more features.
So even if we add totally irrelevant features, R-squared will never decrease. Adj. R-squared penalizes this misleading behavior of R-squared. More details here.
F-statistic and Prob (F-statistic):
These assess the overall significance of a regression model.
They compare the estimated coefficients by OLS with a model whose all coefficients (except for the intercept) are zero.
F-statistic tests whether the independent variables collectively have any effect on the dependent variable or not.
Prob (F-statistic) is the associated p-value with the F-statistic.
A small p-value (typically less than 0.05) indicates that the model as a whole is statistically significant.
This means that at least one independent variable has a significant effect on the dependent variable.
Log-Likelihood:
AIC and BIC:
Like adjusted R-squared, these are performance metrics to determine goodness of fit while penalizing complexity.
Lower AIC and BIC values indicate a better fit. We discussed them here.
The second section provides details related to the features:
coef: The estimated coefficient for a feature.
t and P>|t|:
Earlier, we used F-statistic to determine the statistical significance of the model as a whole.
t-statistic is more granular on that front as it determines the significance of every individual feature.
P>|t| is the associated p-value with the t-statistic.
A small p-value (typically less than 0.05) indicates that the feature is statistically significant.
For instance, the feature “X” has a p-value of ~0.6. This suggests that there is a 60% chance that the feature “X” has no effect on “Y”.
[0.025, 0.975] and std err:
See, the coefficients we have obtained from the model are just estimates. They may not be absolute true coefficients of the process that generated the data.
Thus, the estimated parameters are subject to uncertainty, aren’t they?
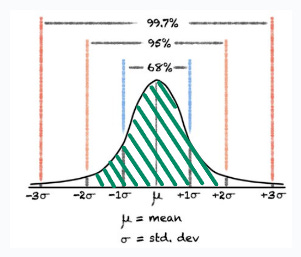
Note: The width of the interval [0.025, 0.975] is 0.95 → or 95%. This constitutes the area between 2 standard deviations from the mean in a normal distribution.
A 95% confidence interval provides a range of values within which you can be 95% confident that the true value of the parameter lies.
For instance, the interval for
sin_Xis(0.092, 6.104). So although the estimated coefficient is3.09, we can be 95% confident that the true coefficient lies in the range(0.092, 6.104).What is a confidence interval? We covered it here.
Details in the last section of the report test the assumptions of linear regression.
Omnibus and Prob(Omnibus):
They test the normality of the residuals.
Omnibus value of zero means residuals are perfectly normal.
Prob(Omnibus) is the corresponding p-value.
In this case, Prob(Omnibus) is 0.001. This means there is a 0.1% chance that the residuals are normally distributed.
Skew and Kurtosis:
They also provide information about the distribution of the residuals.
Skewness measures the asymmetry of the distribution of residuals.
Zero skewness means perfect symmetry.
Positive skewness indicates a distribution with a long right tail. This indicates a concentration of residuals on lower values. Good to check for outliers in this case.
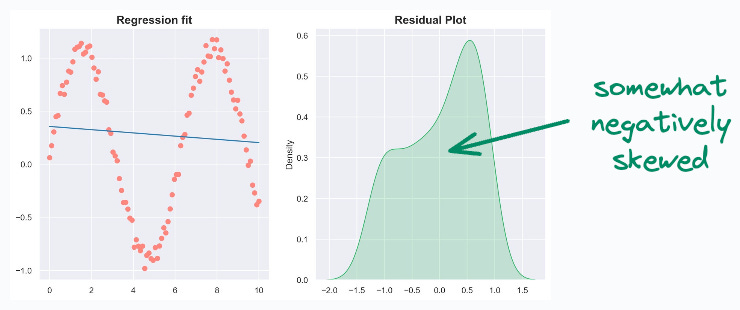
Negative skewness indicates a distribution with a long left tail. This is mostly indicative of poor features. For instance, consider fitting a sin curve with a linear feature (X). Most residuals will be high, resulting in negative skewness.
Durbin-Watson:
This measures autocorrelation between residuals.
Autocorrelation occurs when the residuals are correlated, indicating that the error terms are not independent.
But linear regression assumes that residuals are not correlated.
The Durbin-Watson statistic ranges between
0and4.A value close to 2 indicates no autocorrelation.
Values closer to 0 indicate positive autocorrelation.
Values closer to 4 indicate negative autocorrelation.
Jarque-Bera (JB) and Prob(JB):
They solve the same purpose as Omnibus and Prob(Omnibus) — measuring the normality of residuals.
Condition Number:
This tests multicollinearity.
Multicollinearity occurs when two features are correlated, or two or more features determine the value of another feature.
A standalone value for Condition Number can be difficult to interpret so here’s how I use it:
Add features one by one to the regression model and notice any spikes in the Condition Number.
Done!
See, as discussed above, every section of this report has its importance:
The first section tells us about the model’s config, the overall performance of the model, and its statistical significance.
The second section tells us about the statistical significance of individual features, the model’s confidence in finding the true coefficient, etc.
The last section lets us validate the model’s assumptions, which are immensely critical to linear regression’s performance.
Now you know how to interpret the entire regression summary from statsmodel.
👉 Over to you: What other statistical details do you want me to simplify?
👉 If you liked this post, don’t forget to leave a like ❤️. It helps more people discover this newsletter on Substack and tells me that you appreciate reading these daily insights.
The button is located towards the bottom of this email.
Thanks for reading!










Ey! Don’t stop posting content like this! And very helpful the 4hours vs 2 secs comparison! Here’s my like bro!
I have used linear regression models for 35 years and sometimes very successfull, but this is the first time I see an understandable explanation of all the parameters. Thanks!