The Biggest Limitation Of Pearson Correlation Which Many Overlook

...And what to use instead.

Pearson correlation is commonly used to determine the association between two continuous variables.

Many frameworks (in Pandas, for instance) have it as their default correlation metric.

Yet, unknown to many, Pearson correlation:

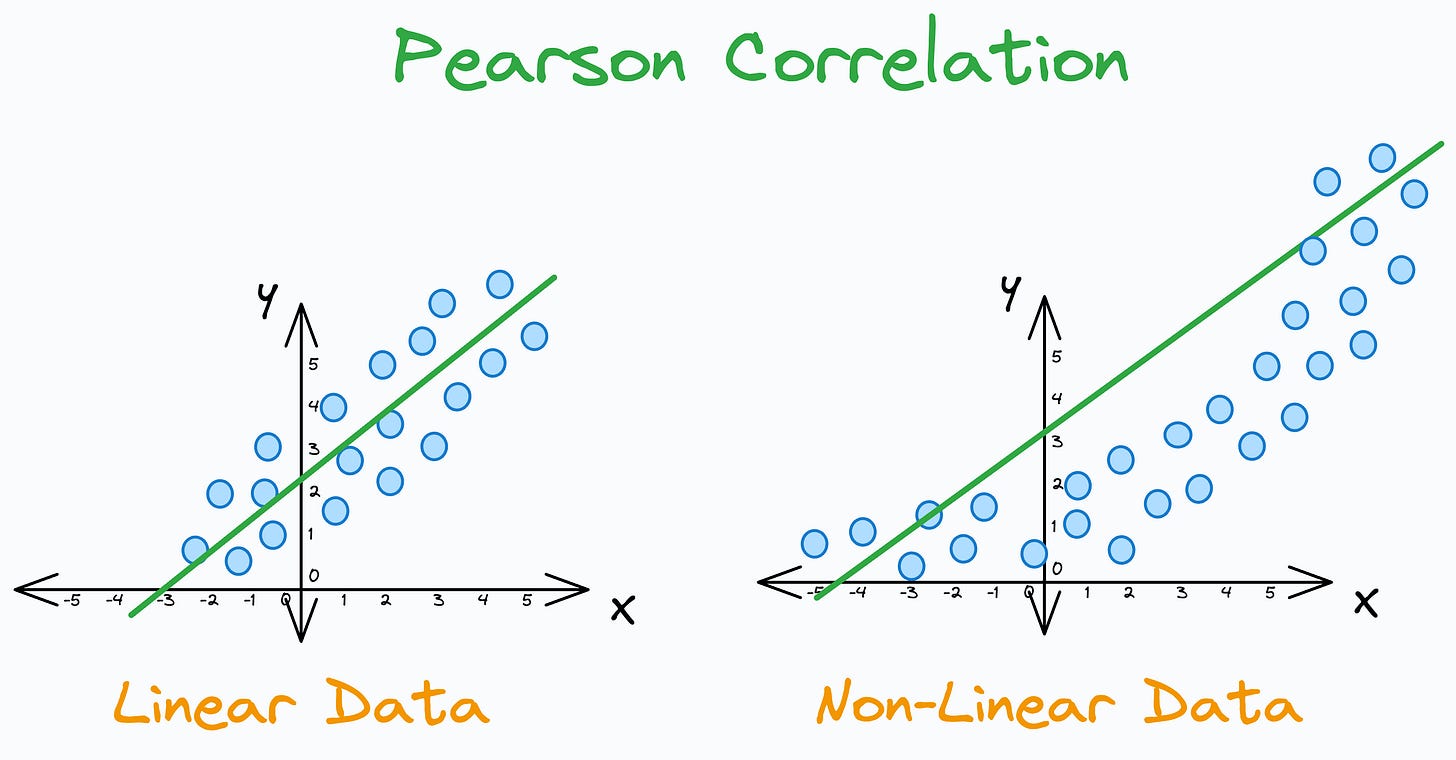
• only measures the linear relationship.

• penalizes a non-linear yet monotonic association.

Pearson correlation only measures the linear relationship

Instead, Spearman correlation is a better alternative.

It assesses monotonicity, which can be linear as well as non-linear.

Monotonicity in data

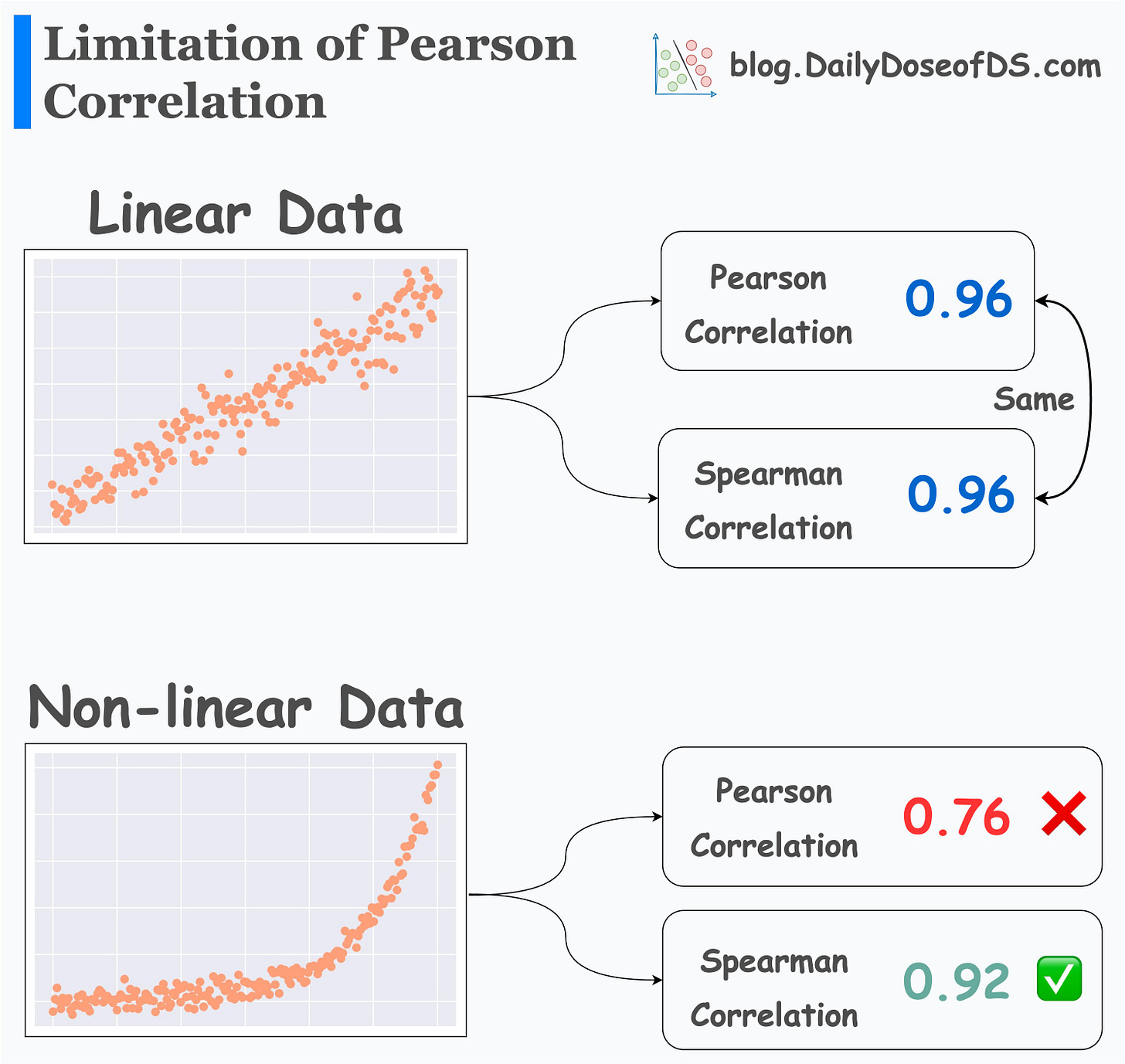
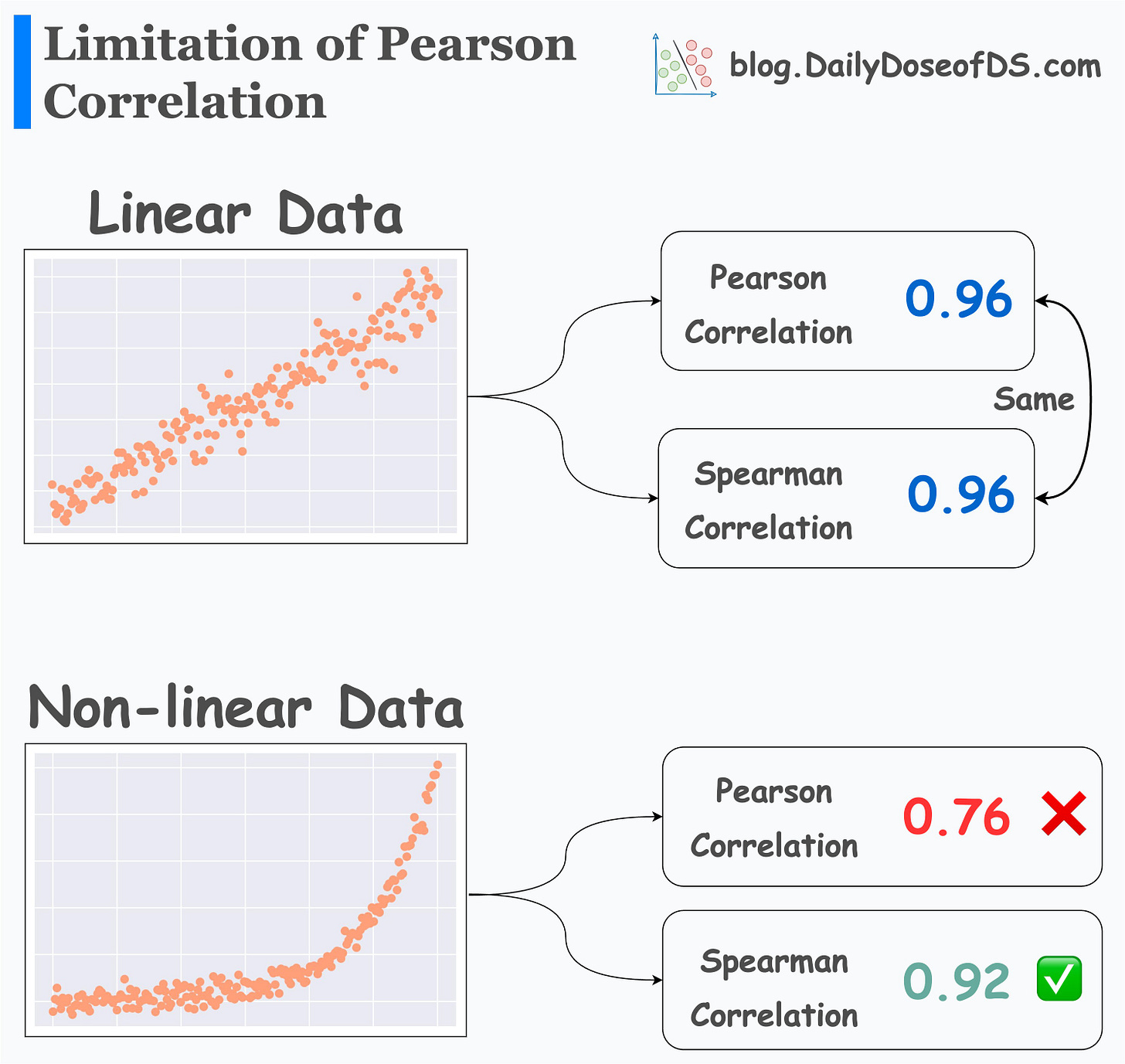
This is evident from the illustration below:

Pearson vs. Spearman on linear and non-linear data

• Pearson and Spearman correlation is the same on linear data.

• But Pearson correlation underestimates a non-linear association.

Spearman correlation is also useful when data is ranked or ordinal.

👉 Over to you: What are some other alternatives that address Pearson's limitations?

👉 If you liked this post, don’t forget to leave a like ❤️. It helps more people discover this newsletter on Substack and tells me that you appreciate reading these daily insights. The button is located towards the bottom of this email.

Thanks for reading!

---

Hey there!

It’s been over a week since I launched the paid memberships. I’m grateful to everyone who has signed up and shown support.

Over the last few days, a few have also approached me to ask for a discount.

So just to clarify, the membership page shows the base pricing. But it may not be applicable to you.

Membership pricing comes with purchasing power parity.

Thus, as shown below, individuals living in countries with lower purchasing powers automatically get prompted with a discount banner.

Membership Page

👉 Check your PPP discount here: Daily Dose of Data Science Membership.

If you need further assistance, you can connect directly via the chat icon on the website here:

Have a good day :)

Avi