The Caveats of Binary Cross Entropy Loss That Aren’t Talked About as Often as They Should Be
...when using it in imbalanced dataset.
Binary classification tasks are typically trained using the binary cross entropy (BCE) loss function:
For notational convenience, if we define pₜ as the following:
…then we can also write the cross-entropy loss function as:
That said, one overlooked limitation of BCE loss is that it weighs probability predictions for both classes equally, which is also evident from the symmetry of the loss function:
For more clarity, consider the table below, which depicts two instances, one from the minority class and another from the majority class, both with the same loss value:
This causes problems when we use BCE for imbalanced datasets, wherein most instances from the dominating class are “easily classifiable.”
Thus, a loss value of, say, -log(0.3) from the majority class instance should (ideally) be weighed LESS than the same loss value from the minority class.
Focal loss is a pretty handy and useful alternative to address this issue. It is defined as follows:
As depicted above, it introduces an additional multiplicative factor called downweighing, and the parameter γ (Gamma) is a hyperparameter.
Plotting BCE (class y=1) and Focal loss (for class y=1 and γ=3), we get the following curve:
As shown in the figure above, focal loss reduces the contribution of the predictions the model is pretty confident about.
Also, the higher the value of γ (Gamma), the more downweighing takes place, which is evident from the plot below:
Moving on, while the Focal loss function reduces the contribution of confident predictions, we aren’t done yet.
If we consider the focal loss function now, we notice that it is still symmetric like BCE:
To address this, we must add another weighing parameter (α), which is the inverse of the class frequency, as depicted below:
Thus, the final loss function comes out to be the following:
By using both downweighing and inverse weighing, the model gradually learns patterns specific to the hard examples instead of always being overly confident in predicting easy instances.
To test the efficacy of focal loss in a class imbalance setting, I created a dummy classification dataset with a 90:10 imbalance ratio:
Next, I trained two neural network models (with the same architecture of 2 hidden layers):
One with BCE loss
Another with Focal loss
The decision region plot and test accuracy for these two models is depicted below:
It is clear that:
The model trained with BCE loss (left) always predicts the majority class.
The model trained with focal loss (right) focuses relatively more on minority class patterns. As a result, it performs better.
Download this Jupyter notebook to get started with Focal loss: Focal loss notebook.
👉 Over to you: What are some other alternatives to BCE loss under class imbalance?
👉 If you liked this post, don’t forget to leave a like ❤️. It helps more people discover this newsletter on Substack and tells me that you appreciate reading these daily insights.
The button is located towards the bottom of this email.
Thanks for reading!
Latest full articles
If you’re not a full subscriber, here’s what you missed last month:
Don’t Stop at Pandas and Sklearn! Get Started with Spark DataFrames and Big Data ML using PySpark.
DBSCAN++: The Faster and Scalable Alternative to DBSCAN Clustering
Federated Learning: A Critical Step Towards Privacy-Preserving Machine Learning
You Cannot Build Large Data Projects Until You Learn Data Version Control!
Sklearn Models are Not Deployment Friendly! Supercharge Them With Tensor Computations.
Deploy, Version Control, and Manage ML Models Right From Your Jupyter Notebook with Modelbit
Gaussian Mixture Models (GMMs): The Flexible Twin of KMeans.
To receive all full articles and support the Daily Dose of Data Science, consider subscribing:
👉 Tell the world what makes this newsletter special for you by leaving a review here :)
👉 If you love reading this newsletter, feel free to share it with friends!








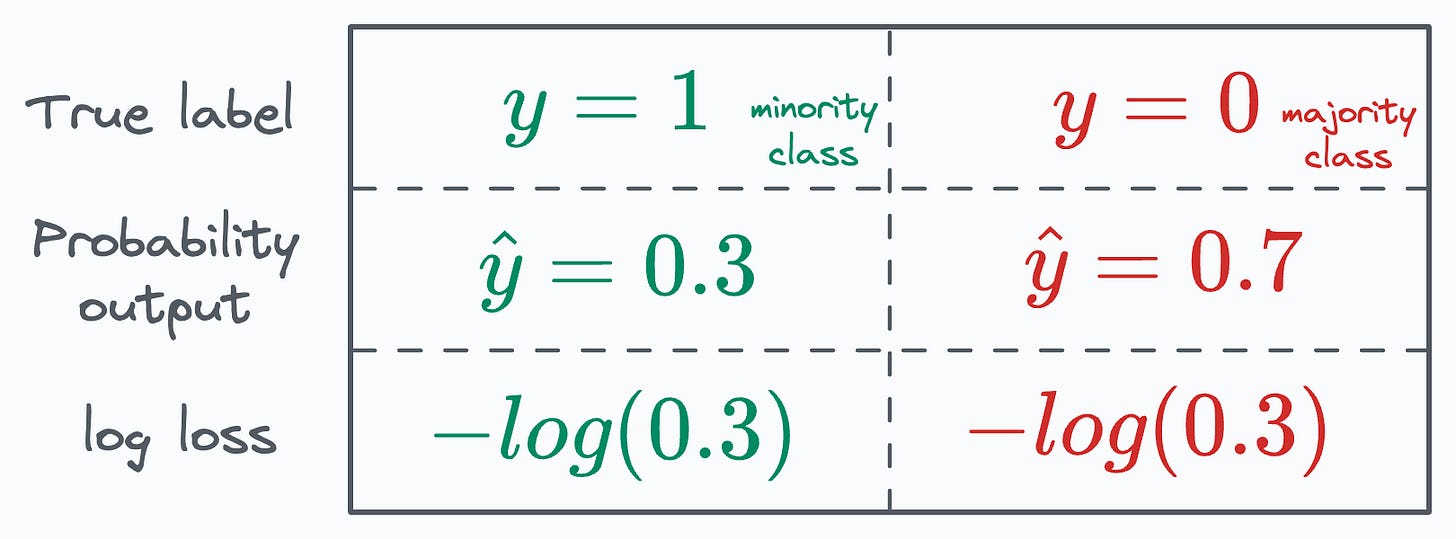










Interesting idea, but maybe we just need to tweak the classification threshold of the first neural net to improve its accuracy.