The Limitation of Pearson Correlation While Using It With Ordinal Categorical Data

...and here’s what to use instead.

Imagine you have an ordinal categorical feature. You want to measure its correlation with other continuous features.

Ordinal feature: Categorical data with a natural ordering in categories

Before proceeding with the correlation analysis, you will encode the feature, which is a fair thing to do.

Encoding ordinal data

Yet, unknown to many, the choice of encoding can largely affect the correlation results.

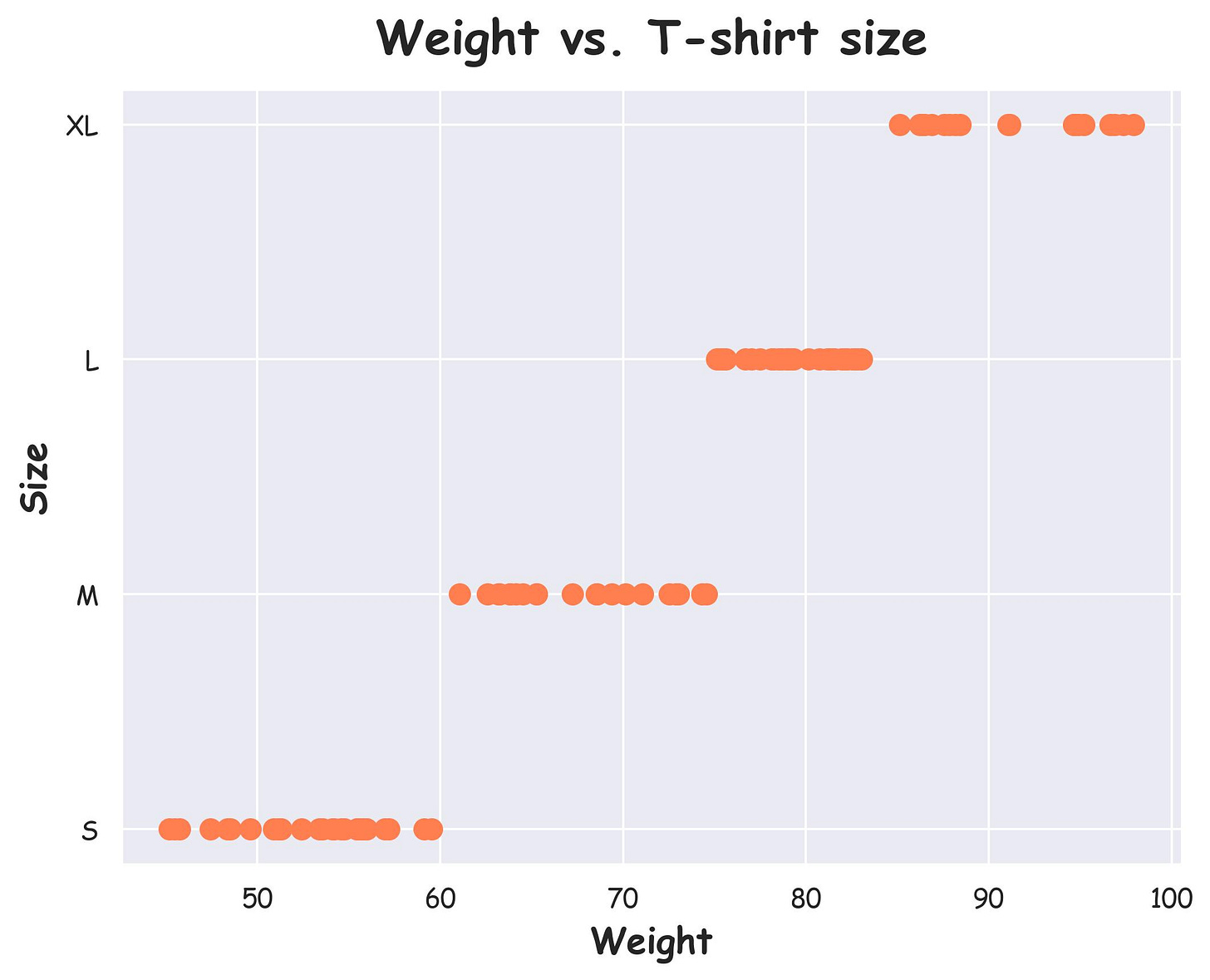
For instance, consider the dataset below:

Weight vs. t-shirt size data

Here, we have:

• An ordinal categorical feature: t-shirt size (S, M, L, XL).

• A continuous feature: weight.

Intuitively, there must be a monotonic relationship between the two features.

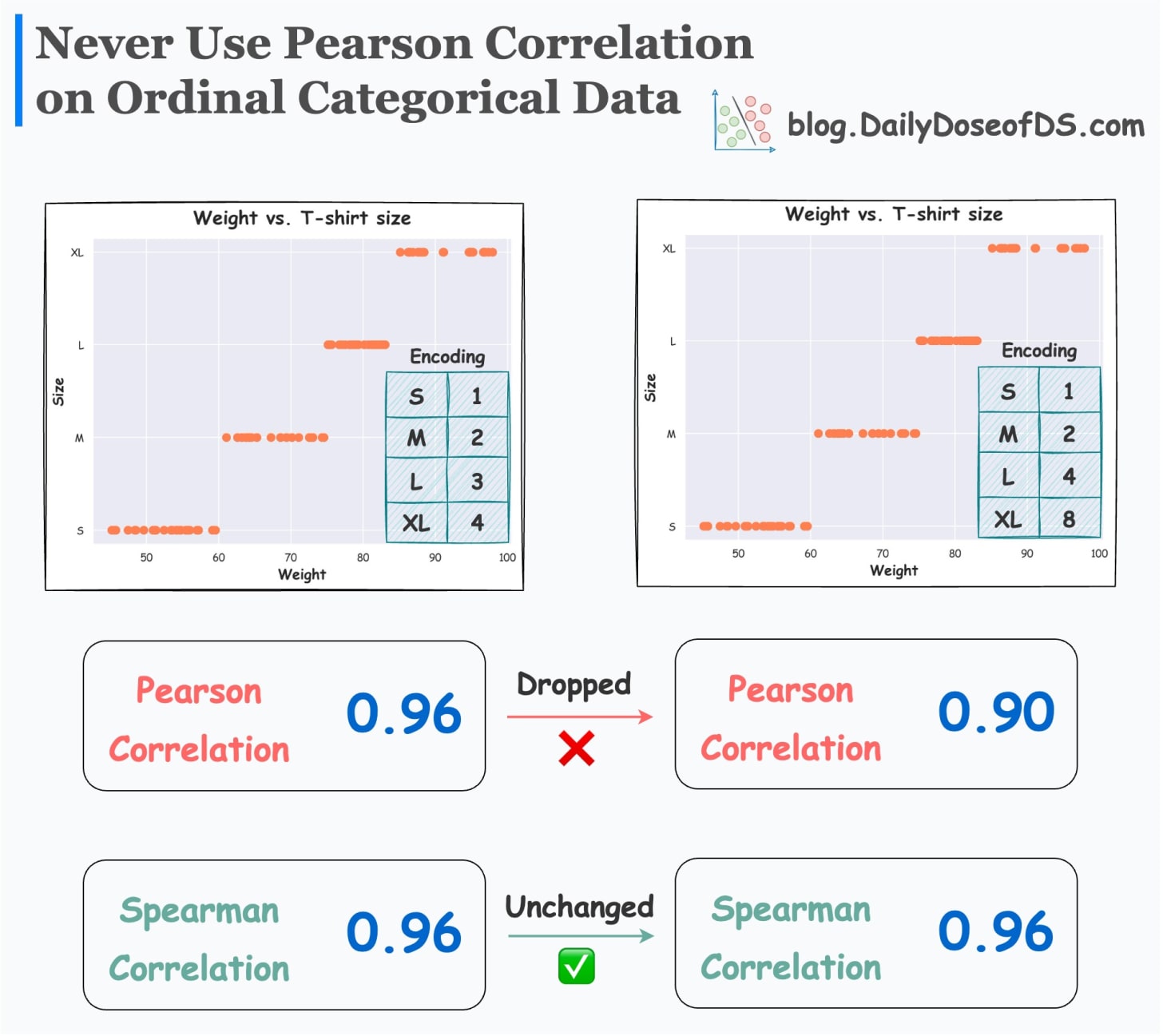
However, as depicted below, altering the categorical encoding affects the Pearson correlation.

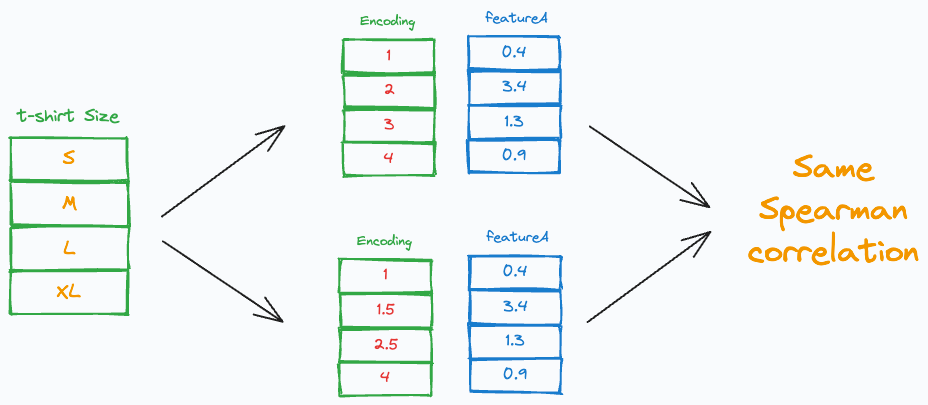
Spearman correlation is a better alternative to assess the monotonicity between ordinal and continuous features.

We also discussed it in an earlier post, when we assessed the correlation between continuous features.

It always remains the same, irrespective of the choice of categorical encoding. This is because the Spearman correlation is rank-based.

Different ordinal encodings result in the same Spearman correlation

It operates on the ranks of the data, which makes it more suitable for such cases of correlation analysis.

Both ordinal encodings have the same rank

👉 Over to you: What are some other measures to determine the correlation between categorical data and continuous data?

👉 If you liked this post, don’t forget to leave a like ❤️. It helps more people discover this newsletter on Substack and tells me that you appreciate reading these daily insights. The button is located towards the bottom of this email.

Thanks for reading!

---

Latest full articles

If you’re not a full subscriber, here’s what you missed last month:

• Formulating and Implementing the t-SNE Algorithm From Scratch.

• Generalized Linear Models (GLMs): The Supercharged Linear Regression.

• Gaussian Mixture Models (GMMs): The Flexible Twin of KMeans.

• Bayesian Optimization for Hyperparameter Tuning.

• Formulating the PCA Algorithm From Scratch.

• Where Did The Assumptions of Linear Regression Originate From?

To receive all full articles and support the Daily Dose of Data Science, consider subscribing:

---

👉 Tell the world what makes this newsletter special for you by leaving a review here :)

👉 If you love reading this newsletter, feel free to share it with friends!