The Ultimate Comparison Between PCA and t-SNE Algorithm

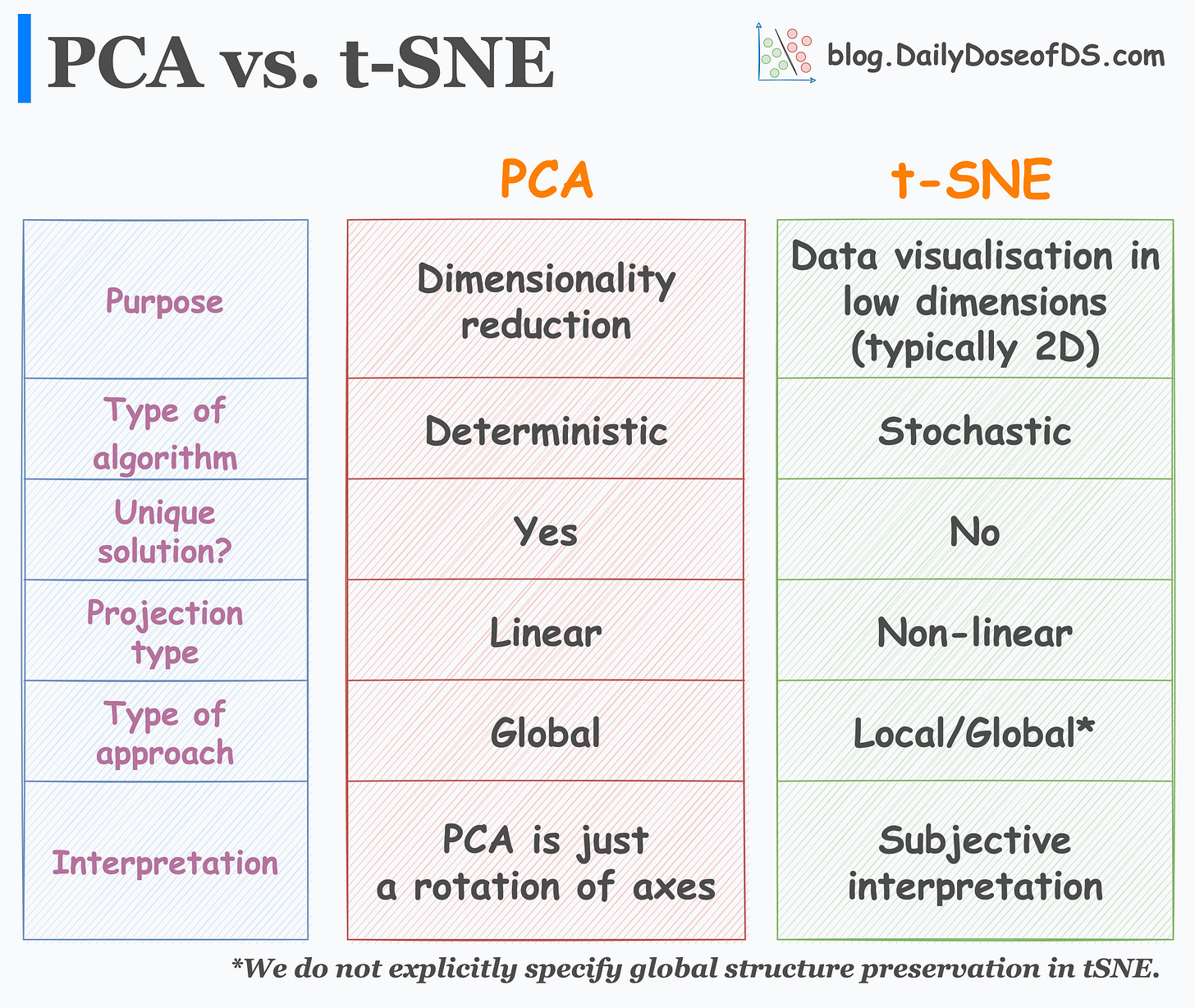
Comparing both algorithms on six parameters.

Avi Chawla

Oct 05, 2023

In earlier newsletter issues, we discussed PCA and t-SNE individually.

Yet, a formal comparison between the two approaches is still left to be covered.

Let’s do it today.

The visual below neatly summarizes the major differences between the two algorithms:

First and foremost, let’s understand their purpose:

While many interpret PCA as a data visualization algorithm, it is primarily a dimensionality reduction algorithm.
t-SNE, however, is a data visualization algorithm. We use it to project high-dimensional data to low dimensions (primarily 2D).

Moving on:

PCA is a deterministic algorithm. Thus, if we run the algorithm twice on the same dataset, we will ALWAYS get the same result.
t-SNE, however, is a stochastic algorithm. Thus, rerunning the algorithm can lead to entirely different results. Can you explain why? Share your answers :)

As far as uniqueness and interpretation of results is concerned:

PCA always has a unique solution for the projection of data points. Simply put, PCA is just a rotation of axes such that the new features we get are uncorrelated.
t-SNE, as discussed above, can provide entirely different results, and its interpretation is subjective in nature.

Next, how do they project data?

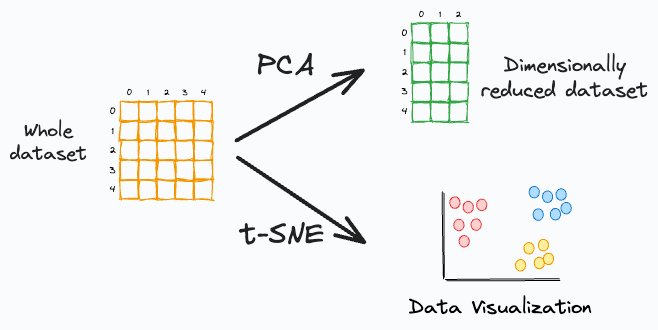
PCA is a linear dimensionality reduction approach. Thus, it is not well-suited if we have a non-linear dataset (which is often true), as shown below:

t-SNE is a non-linear approach. It can handle non-linear datasets.

During dimensionality reduction:

PCA only aims to retain the global variance of the data. Thus, local relationships (such as clusters) are often lost after projection, as shown below:

PCA does not preserve local relationships

t-SNE preserves local relationships. Thus, data points in a cluster in the high-dimensional space are much more likely to lie together in the low-dimensional space.
- In t-SNE, we do not explicitly specify global structure preservation. But it typically does create well-separated clusters.
- Nonetheless, it is important to note that the distance between two clusters in low-dimensional space is NEVER an indicator of cluster separation in high-dimensional space.

If you are interested in learning more about their motivation, mathematics, custom implementations, limitations, etc., feel free to read these two in-depth articles:

👉 Over to you: What other differences between t-SNE and PCA did I miss?

👉 If you liked this post, don’t forget to leave a like ❤️. It helps more people discover this newsletter on Substack and tells me that you appreciate reading these daily insights. The button is located towards the bottom of this email.

Thanks for reading!