Top Gradient Boosting Methods

...summarized for ML engineers.

Meta’s latest open-source updates for ML engineers!

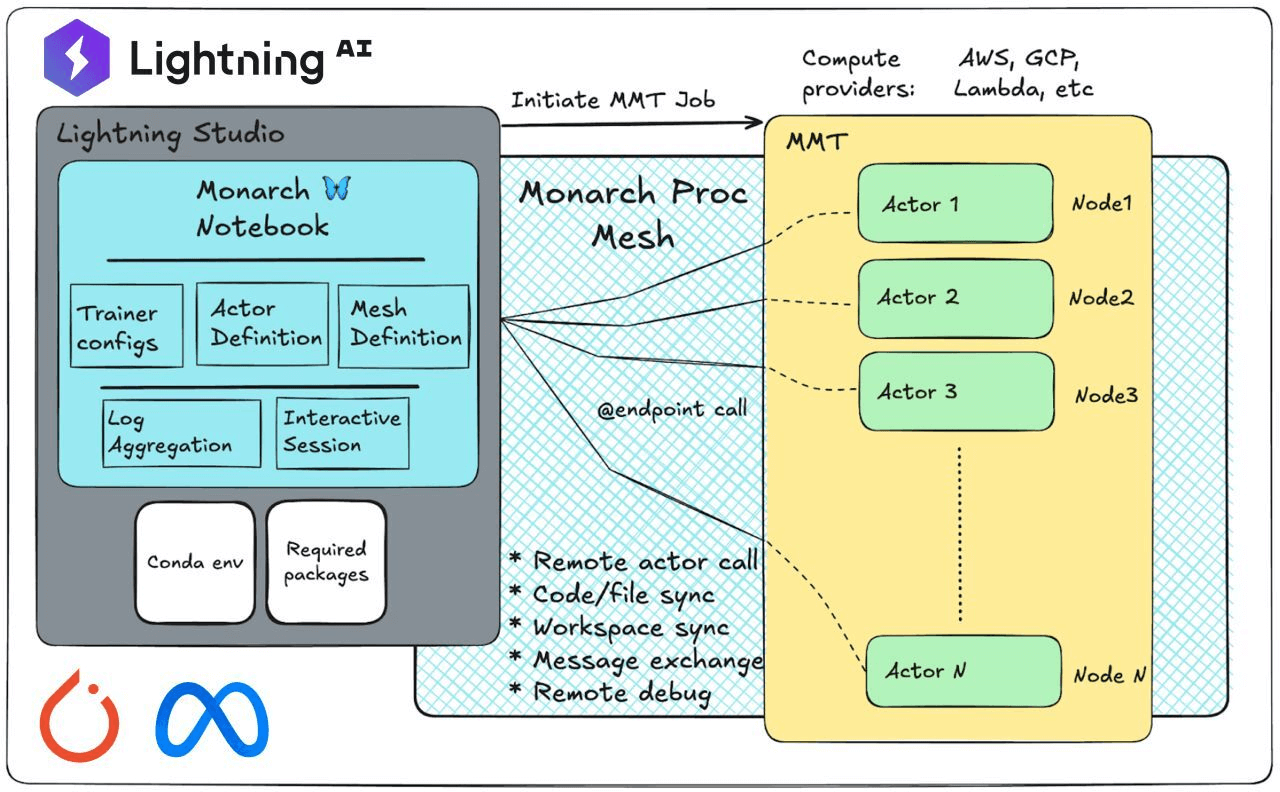
Meta AI just launched Monarch, torchforge, and OpenEnv for PyTorch developers and researchers.

Lightning collaborated with the PyTorch team at Meta to launch a suite of tools, including an AI Code Editor, Lightning Environments Hub, and deep integrations with these new frameworks, all built to accelerate distributed training, reinforcement learning, and experimentation.

If you’re a PyTorch developer, you need to check these:

Large-scale training with Monarch →

OpenEnv quickstart →

---

Top Gradient Boosting Methods

In the early 2000s, Jerome Friedman showed that one can build a strong prediction model by adding weak learners in the direction of the steepest descent of a loss function.

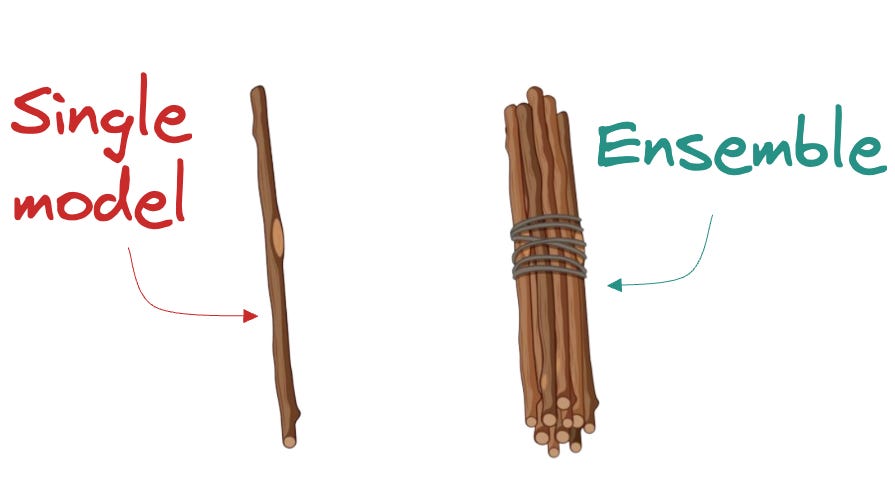
This insight laid the foundation for a whole lot of gradient-boosting tools and ensemble methods that now dominate ML competitions and production pipelines.

This visual is an intuitive way to understand why ensembles are powerful:

Below, we have curated a list of widely used gradient‑boosting libraries and frameworks, along with what makes the tool special, and highlight research papers from top journals that have used the tool to solve real-world problems.

Let’s begin!

---

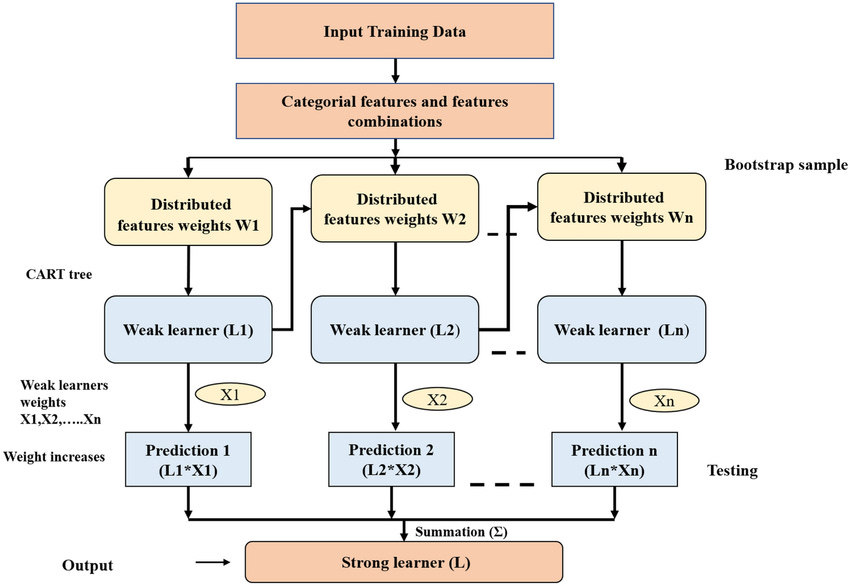
XGBoost

eXtreme Gradient Boosting (XGBoost) is an open‑source framework famous for winning Kaggle competitions and for its scalability, regularization options, and outstanding performance on structured data.

XGBoost is one of the first tree-based models to mathematically formalize the concept of complexity in a tree, which leads to more optimal pruning.

In fact, if you browse Kaggle leaderboards or industry case studies, XGBoost shows up again and again. It’s fast, supports customized loss functions, and integrates with Python, R, Scala, and Java.

Here are some notable papers:

• Dataset Distillation: A Comprehensive Review: This survey on data-efficient learning utilizes XGBoost as a canonical reference for scalability and efficiency, and as an ML baseline, highlighting its ongoing importance.

• Making Efficient, Interpretable, and Fair Models for Healthcare: This paper utilized XGBoost in performance and interpretability comparisons for developing fair and transparent models in digital health. It impacts both fairness research and the adoption of clinical ML pipelines.

• Explainable ML for credit risk analysis: Demonstrates how XGBoost is used in the finance industry for interpretable lending and risk models.

CatBoost

Categorical Boosting (CatBoost) was developed by Yandex, and it is probably the easiest supervised learning algorithm to use today on large tabular data.

• It is highly parallelizable.

• It automatically deals with missing values and categorical variables.

• It is built to prevent overfitting (even more than XGBoost).

If you throw some data into it, without much work, you are pretty much guaranteed to get great results. This assumes your data is training-ready, but even then, it is almost too good to be true!

At its core, it uses ordered boosting and ordered target encoding to avoid target leakage and builds symmetric trees to improve generalization.

The framework also provides robust GPU support.

Here are some notable papers:

• CatBoost: unbiased boosting with categorical features: This is CatBoost’s foundational paper explaining its unique innovation for categorical data.

• Tabular Data: Deep Learning is Not All You Need: This is one of the most cited recent papers on tabular data benchmarks CatBoost, XGBoost, LightGBM, and a range of deep learning models. The paper shows that gradient boosting models (including CatBoost) dominate tabular data tasks. It spurred significant discussion and follow-up work in ML on tabular data.

• A comparative study of CatBoost and XGBoost on feature selection techniques for cancer classification: The paper compares leading ML approaches in cancer genomics, demonstrating CatBoost’s competitive performance for cancer classification, influencing feature selection and classification research for health and bioinformatics. It also compares CatBoost vs. XGBoost in biomedical datasets. Lastly, it shows CatBoost’s real-world impact beyond classical ML research, directly influencing how features and algorithms are selected in health and genomics research.

LightGBM

Light Gradient Boosting Machine (LightGBM) was developed by Microsoft, and they made some tweaks to XGBoost.

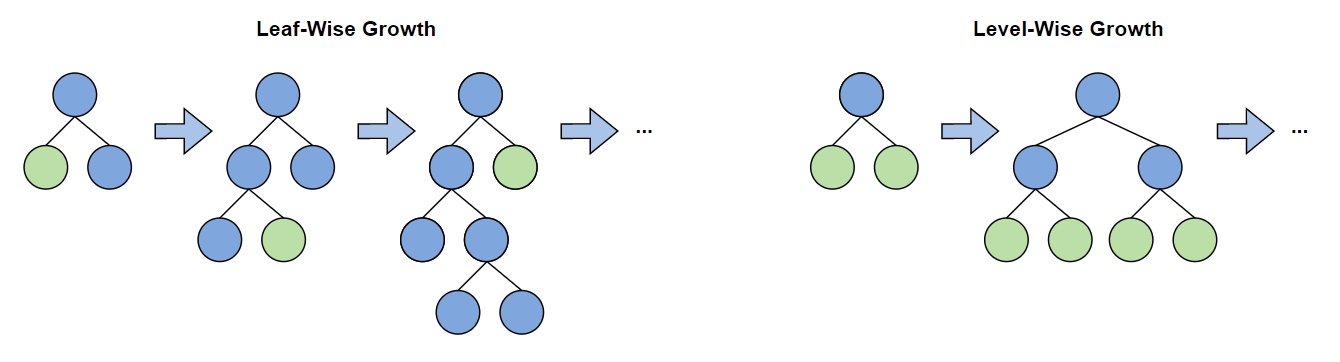
Firstly, instead of the level‑wise growth used in XGBoost, it used a leaf‑wise (best‑first) tree‑growth strategy.

The produced smaller trees and trained faster, especially on large and high‑dimensional datasets, while also handling categorical features natively.

Moreover, it employed techniques like Gradient‑based One‑Side Sampling (GOSS) and Exclusive Feature Bundling (EFB) to reduce the number of data points and features considered at each split.

Here are some notable papers:

• LightGBM: A Highly Efficient Gradient Boosting Decision Tree: This is the original paper that describes LightGBM’s innovations, which are its histogram-based algorithm and real-world scaling.

• High-Throughput Phenotyping with LightGBM for Automated Disease Detection in Agriculture: In this paper, the authors used LightGBM for crop disease detection, showing an impact in precision agriculture.

• Explainable machine learning for early diagnosis of sepsis in ICU patients: The authors built an explainable LightGBM model for early sepsis detection in ICU patients, achieving high recall and providing interpretable feature importance using SHAP.

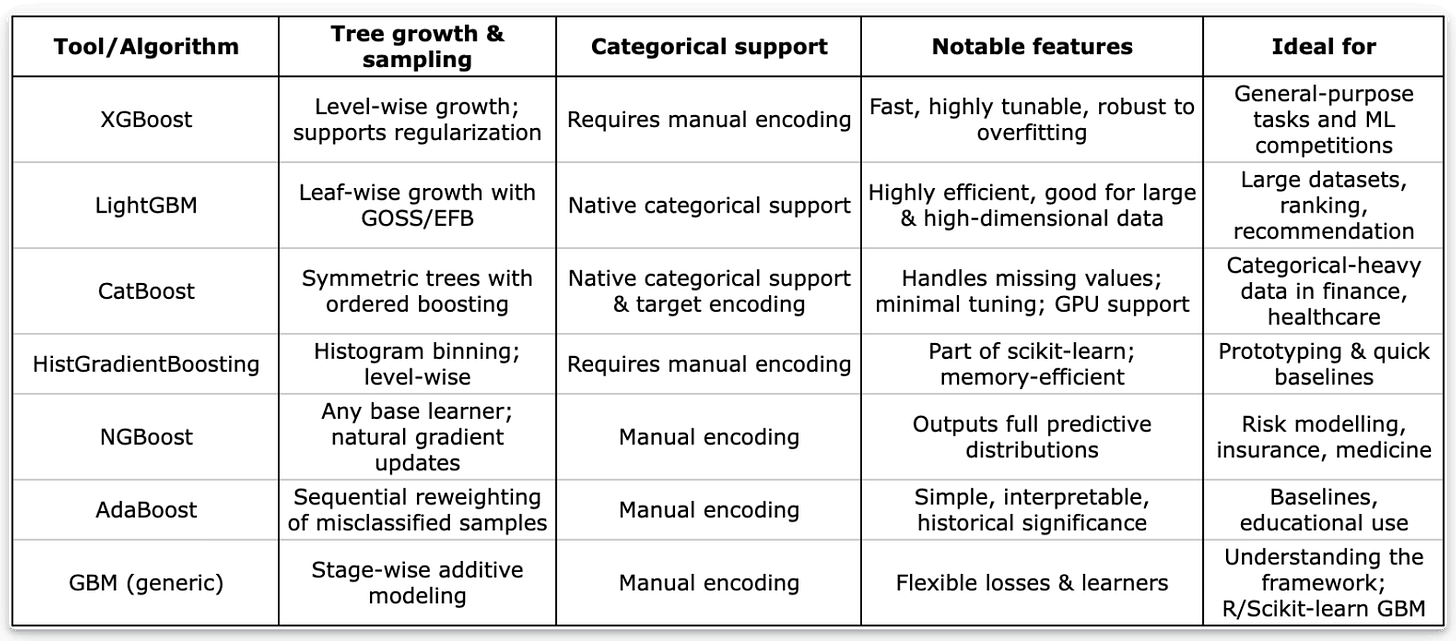
XGBoost vs LightGBM vs CatBoost

Here’s how they differ and when to use which:

• Handling categorical features:

  • XGBoost: Doesn’t natively handle categorical features, so you’ll need to one-hot or label-encode manually.

  • LightGBM: Accepts categorical columns directly and automatically finds optimal splits.

  • CatBoost: The clear winner here since it uses an advanced combination of target and one-hot encoding internally.

• Missing values:

  • XGBoost: Has built-in support and learns the best direction for missing splits.

  • LightGBM: Treats missing values as their own category during training.

  • CatBoost: Handles missing numeric values well, but categorical nulls need a bit more care.

• Tree growth strategy:

  • XGBoost: Grows trees level-wise (depth by depth).

  • LightGBM: Uses a leaf-wise strategy, faster but more prone to overfitting if not regularized.

  • CatBoost: Grows symmetric trees that are balanced, and often better for generalization.

• Split-finding algorithms:

  • XGBoost: Classic greedy search, optimized for sparsity.

  • LightGBM: Uses GOSS (Gradient-based One-Side Sampling) to skip less-informative samples.

  • CatBoost: Uses MVS (Minimal Variance Sampling) to produce more stable splits.

• GPU & distributed support

  • XGBoost: Full support for distributed and GPU training.

  • LightGBM: Excellent GPU efficiency, which is great for large datasets.

  • CatBoost: GPU support via task_type=’GPU’, but setup can require extra tuning.

• Quick recommendation

  • Choose CatBoost → heavy categorical data or minimal tuning.

  • Choose LightGBM → speed and scalability for large datasets.

  • Choose XGBoost → fine-grained control and consistent performance.

Here’s one more algorithm that extends gradient boosting to probabilistic predictions.

NGBoost

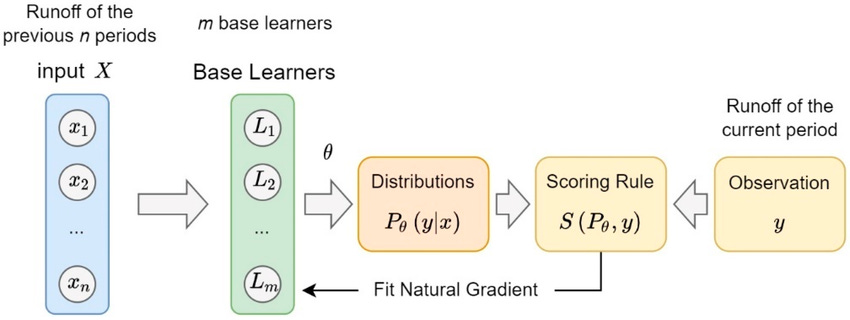
Natural Gradient Boosting( NGBoost) was developed by Stanford, and it extends gradient boosting to probabilistic predictions.

Essentially, instead of producing point estimates, NGBoost models entire probability distributions by updating base learners using the natural gradient.

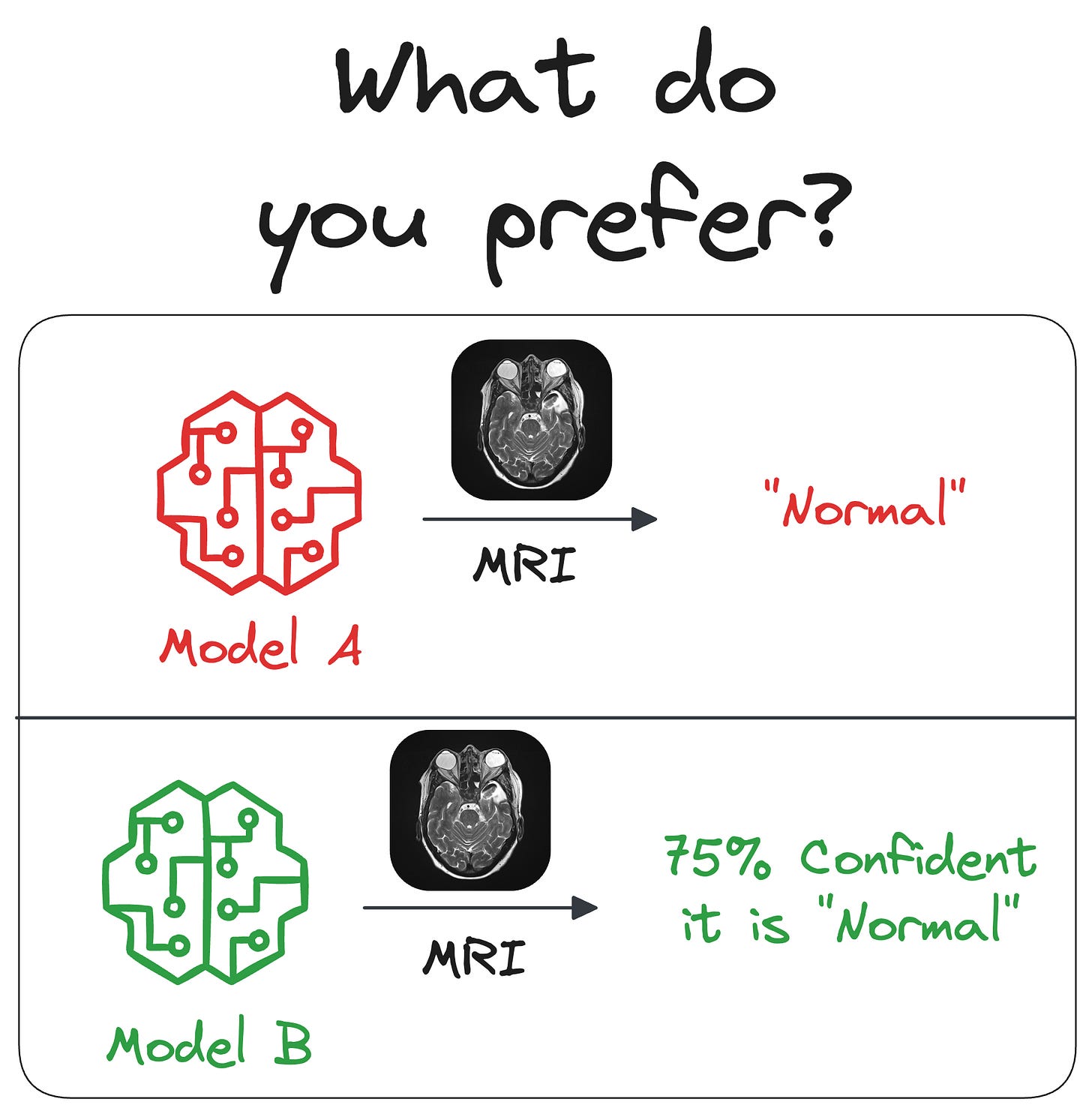
This approach provides uncertainty estimates alongside predictions (like prediction intervals do).

This is super important for domains like insurance, finance and healthcare, where understanding uncertainty is as important as predicting the mean.

NGBoost enables richer decision‑making by quantifying predictive distributions rather than just point estimates.

Here are some notable papers:

• NGBoost: Natural Gradient Boosting for Probabilistic Prediction: This is the original paper proposing NGBoost. It formalizes how boosting can be extended to probabilistic regression by treating the distribution parameters (e.g., mean, variance) as the targets.

• An Explainable Nature-Inspired Framework for Monkeypox Diagnosis: This paper fuses deep feature extraction (via Xception CNN) with NGBoost for classification. The paper reports high performance (accuracy, AUC) and uses explanation techniques (e.g., Grad-CAM, LIME) to provide interpretability.

• From Point to probabilistic gradient boosting for claim frequency and severity prediction: This paper compares NGBoost with many modern boosting frameworks (GBM, XGBoost, LightGBM, XGBoostLSS, etc.) in actuarial datasets (insurance / claims modeling) to study trade-offs between predictive accuracy, computational cost, and distributional adequacy. This is a strong comparative reference for showing NGBoost’s competitive standing in real-world use.

---

Of course, there are not the only gradient boosting methods. We’ve added a few more algorithms that extend or specialize the original gradient boosting framework, each with unique design choices that make them well-suited for different types of data and use cases.

---

Conclusion

If you consider the last decade (or 12-13 years) in machine learning, neural networks have quite clearly dominated the narrative in many discussions, often being seen as the go-to approach for a wide range of problems.

In contrast, tree-based methods tend to be perceived as more straightforward, and as a result, they don’t always receive the same level of admiration.

However, in practice, tree-based methods frequently outperform neural networks, particularly in structured data tasks.

One would spend a fraction of the time they would otherwise spend on models like linear/logistic regression, SVMs, etc., to achieve the same performance with gradient boosting models.

Thanks for reading!