Use Histograms with Caution
They can be misleading.
Histograms are quite common in data analysis and visualization.
Yet, they can be highly misleading at times.
Why?
Let’s understand today!
To begin, a histogram represents an aggregation of one-dimensional data points based on a specific bin width:
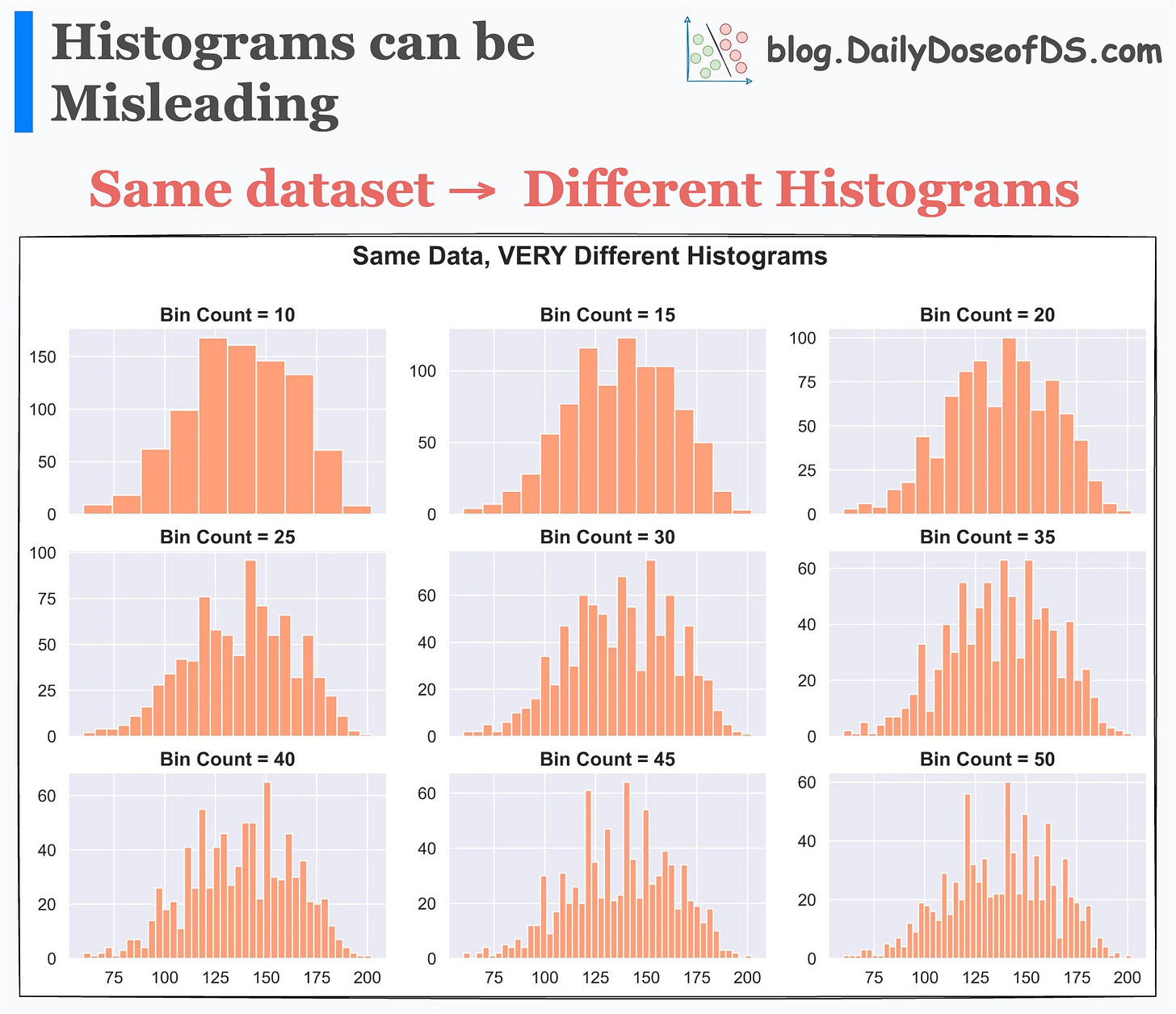
This means that setting different bin widths on the same dataset can generate entirely different histograms.
This is evident from the image below:
Each histogram conveys a different story, even though the underlying data is the same.
Thus, solely looking at a histogram to understand the data distribution may lead to incorrect or misleading conclusions.
Here, the takeaway is not that histograms should not be used. Instead, it is that Whenever you generate any summary statistic, you lose essential information.
In our case, every bin of a histogram also represents a summary statistic — an aggregated count.
And whenever you generate any summary statistic, you lose essential information.
Thus, it is always important to look at the underlying data distribution.
For instance, to understand the data distribution, I prefer a violin (or KDE) plot. This gives me better clarity of data distribution over a histogram.
Visualizing density provides more information and clarity about the data distribution than a histogram.
That said, we covered 8 more pitfalls in data science and the cautionary measures you can take here: 8 Fatal (Yet Non-obvious) Pitfalls and Cautionary Measures in Data Science.
👉 Over to you: What other measures do you take when using summary statistics?
Thanks for reading!
Extended piece #1
There are many issues with Grid search and random search.
They are computationally expensive due to exhaustive search.
The search is restricted to the specified hyperparameter range. But what if the ideal hyperparameter exists outside that range?
They can ONLY perform discrete searches, even if the hyperparameter is continuous.
Bayesian optimization solves this.
It’s fast, informed, and performant, as depicted below:
Learning about optimized hyperparameter tuning and utilizing it will be extremely helpful to you if you wish to build large ML models quickly.
👉 Read it here: Bayesian Optimization for Hyperparameter Tuning.
Extended piece #2
Linear regression is powerful, but it makes some strict assumptions about the type of data it can model, as depicted below.
Can you be sure that these assumptions will never break?
Nothing stops real-world datasets from violating these assumptions.
That is why being aware of linear regression’s extensions is immensely important.
Generalized linear models (GLMs) precisely do that.
They relax the assumptions of linear regression to make linear models more adaptable to real-world datasets.
👉 Read it here: Generalized linear models (GLMs).
Are you preparing for ML/DS interviews or want to upskill at your current job?
Every week, I publish in-depth ML dives. The topics align with the practical skills that typical ML/DS roles demand.
Join below to unlock all full articles:
👉 If you love reading this newsletter, share it with friends!
👉 Tell the world what makes this newsletter special for you by leaving a review here :)