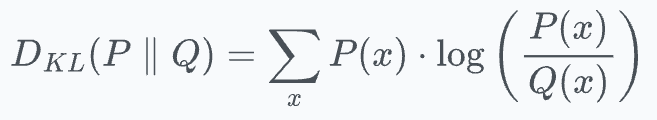What is Early Exaggeration in tSNE?
...and a way to improve it.
If you know how tSNE works (read this 30-minute deep dive if you don’t), you may have noticed that it has an early_exaggeration parameter, as shown below:
What is it, and how does it help?
What does “early” mean in
early_exaggeration?
Let’s understand this today, along with a potential strategy to improve early_exaggeration in tSNE.
Let’s begin!
A brief about tSNE
To understand early exaggeration, we need to briefly overview how tSNE works.
The steps below have been discussed in a mathematical manner here: Formulating and Implementing the t-SNE Algorithm From Scratch.
Step 1) For every point (
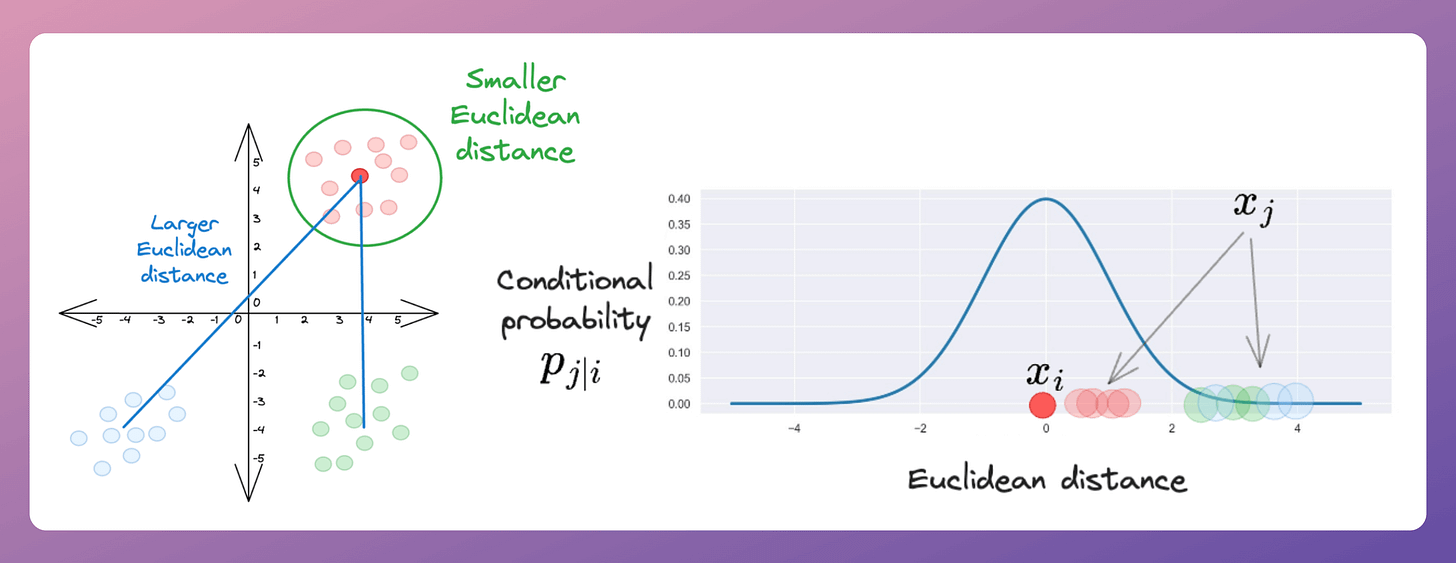
i) in the given high-dimensional data, convert the high-dimensional Euclidean distances to all other points (j) into conditional Gaussian probabilities.For instance, consider the marked red point in the dataset on the left below.
Converting Euclidean distance to all other points into Gaussian probabilities (the distribution on the right above) shows that other red points have a higher probability of being its neighbor than other points.
Step 2) For every data point xᵢ, randomly initialize its counterpart yᵢ in 2-dimensional space. These will be our projections.
Step 3) Just like we defined conditional probabilities in the high-dimensional space in Step 1, we define the conditional probabilities in the low-dimensional space, using Gaussian distribution again.
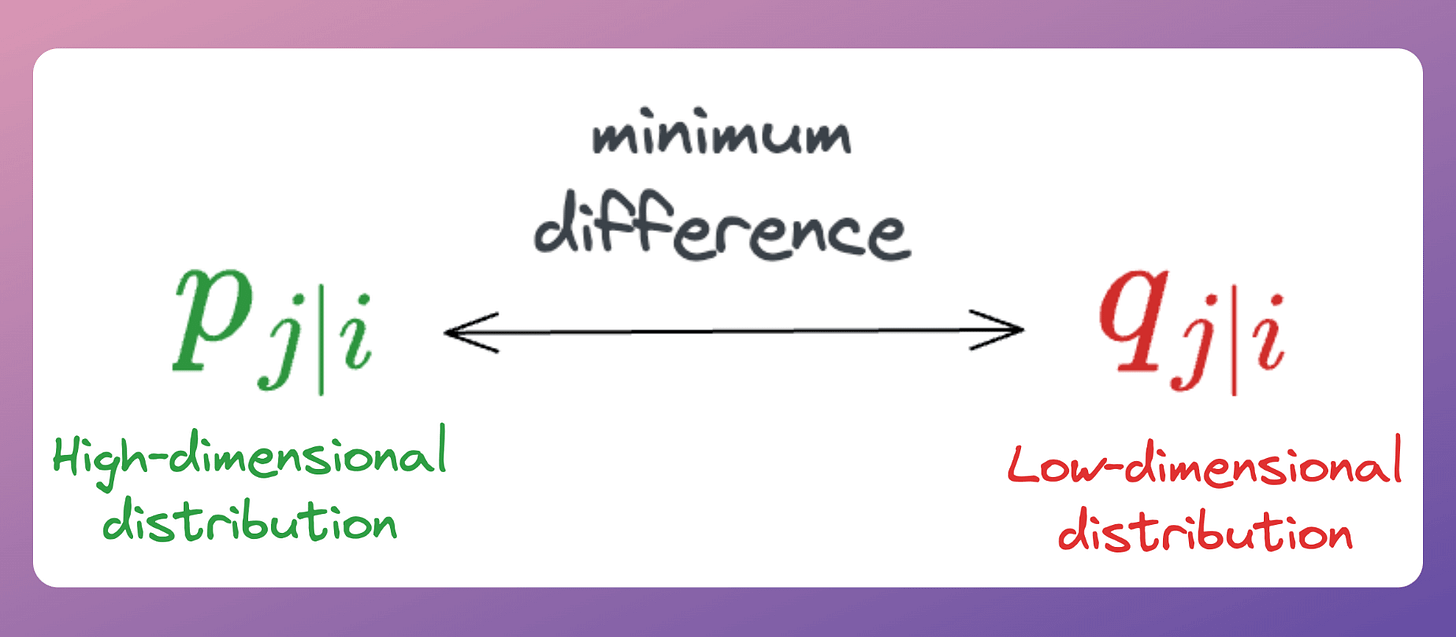
Step 4) Now, every data point (i) has a high-dimensional probability distribution and a corresponding low-dimensional distribution:
The objective is to match these two probability distributions.
Thus, we can make the positions of counterpart yᵢ’s learnable such that this difference is minimized.
Using KL divergence as a loss function helps us achieve this. It measures how much information is lost when we use distribution
Qto approximate distributionP.
Ideally, we want to have the minimum loss value (which is zero), and this will be achieved when
P=Q.
The model can be trained using gradient descent, and it works pretty well.
But having early exaggeration makes it even better.
Early exaggeration
As the name suggests, the idea is to exaggerate (inflate) the values of all high-dimensional conditional Gaussian probabilities (P) during the initial stages of the optimization. That is why the name “Early” exaggeration.
This is achieved by multiplying all high-dimensional Gaussian probabilities (P) by a constant factor greater than 1, as follows:
Here’s why early exaggeration makes sense.
Recall that KL divergence will be minimum only when the distribution P and Q are identical.
Thus, by increasing the values of P, the optimization process is encouraged to learn larger values of Q (since both must be equal if the loss has to be minimum).
As a result, the low-dimensional clusters created will be very tight, and all individual clusters will be widely separated from each other.
In other words, since P is large, this means data points close to each other will have a higher probability of being neighbors in the low-dimensional space as well.
Thus, due to the nature of KL divergence, even the low-dimensional probabilities Q are forced to become large, leading to tightly packed clusters.
This is why we use early exaggeration.
Improving early exaggeration
While tSNE does not use what I am about to share, this is a way early exaggeration could have been implemented and possibly improved as well.
Recall that in early exaggeration, we multiply ALL high-dimensional Gaussian probabilities (P) by a constant factor greater than 1.
While this inflates the joint probability of data points that are very close (likely in the same cluster), the disadvantage is that it also increases the joint probability of data points that are far (likely in different clusters).
An optimal way of doing this could have been to set a threshold (λ) for inflating the joint probabilities.
Thus, we exaggerate the joint probabilities if they exceed a certain threshold.
Otherwise, we understate (or reduce) them.
This makes intuitive sense as well.
This is how early exaggeration works and why it is so useful in tSNE.
One thing to note is that tSNE is an improved version of the SNE algorithm, both used for dimensionality reduction.
The authors introduced several optimizations that led to tSNE, and the difference in the result is evident from the image above.
We went into much more detail about tSNE in a beginner-friendly manner in the full article: Formulating and Implementing the t-SNE Algorithm From Scratch.
This article covers:
The limitations of PCA.
The entire end-to-end working of the SNE algorithm (an earlier version of t-SNE).
What does SNE try to optimize?
What are local and global structures?
Understanding the idea of
perplexityvisually.The limitations of the SNE algorithm.
How is t-SNE different from SNE?
Advanced optimization methods used in t-SNE.
Implementing the entire t-SNE algorithm by only using NumPy.
A practice Jupyter notebook for you to implement t-SNE yourself.
Understanding some potential gaps in t-SNE and how to possibly improve it.
PCA vs. t-SNE comparison.
Limitations of t-SNE.
Why is
perplexitythe most important hyperparameter of t-SNE?Important takeaways for using t-SNE.
Similar to this, we also formulated the PCA algorithm from scratch here: Formulating the Principal Component Analysis (PCA) Algorithm From Scratch.
👉 Over to you: Can you identify a bottleneck in the t-SNE algorithm?
For those who want to build a career in DS/ML on core expertise, not fleeting trends:
Every week, I publish no-fluff deep dives on topics that truly matter to your skills for ML/DS roles.
For instance:
Conformal Predictions: Build Confidence in Your ML Model’s Predictions
Quantization: Optimize ML Models to Run Them on Tiny Hardware
5 Must-Know Ways to Test ML Models in Production (Implementation Included)
Implementing Parallelized CUDA Programs From Scratch Using CUDA Programming
And many many more.
Join below to unlock all full articles:
SPONSOR US
Get your product in front of 88,000 data scientists and other tech professionals.
Our newsletter puts your products and services directly in front of an audience that matters — thousands of leaders, senior data scientists, machine learning engineers, data analysts, etc., who have influence over significant tech decisions and big purchases.
To ensure your product reaches this influential audience, reserve your space here or reply to this email to ensure your product reaches this influential audience.