What Makes Euclidean Distance a Misleading Choice for Distance Metric?
...And a possible alternative to look for.
Euclidean distance is the most commonly used distance metric.
Yet, during its distance calculation, Euclidean distance assumes independent axes.
Thus, if your features are correlated, Euclidean distance will produce misleading results.
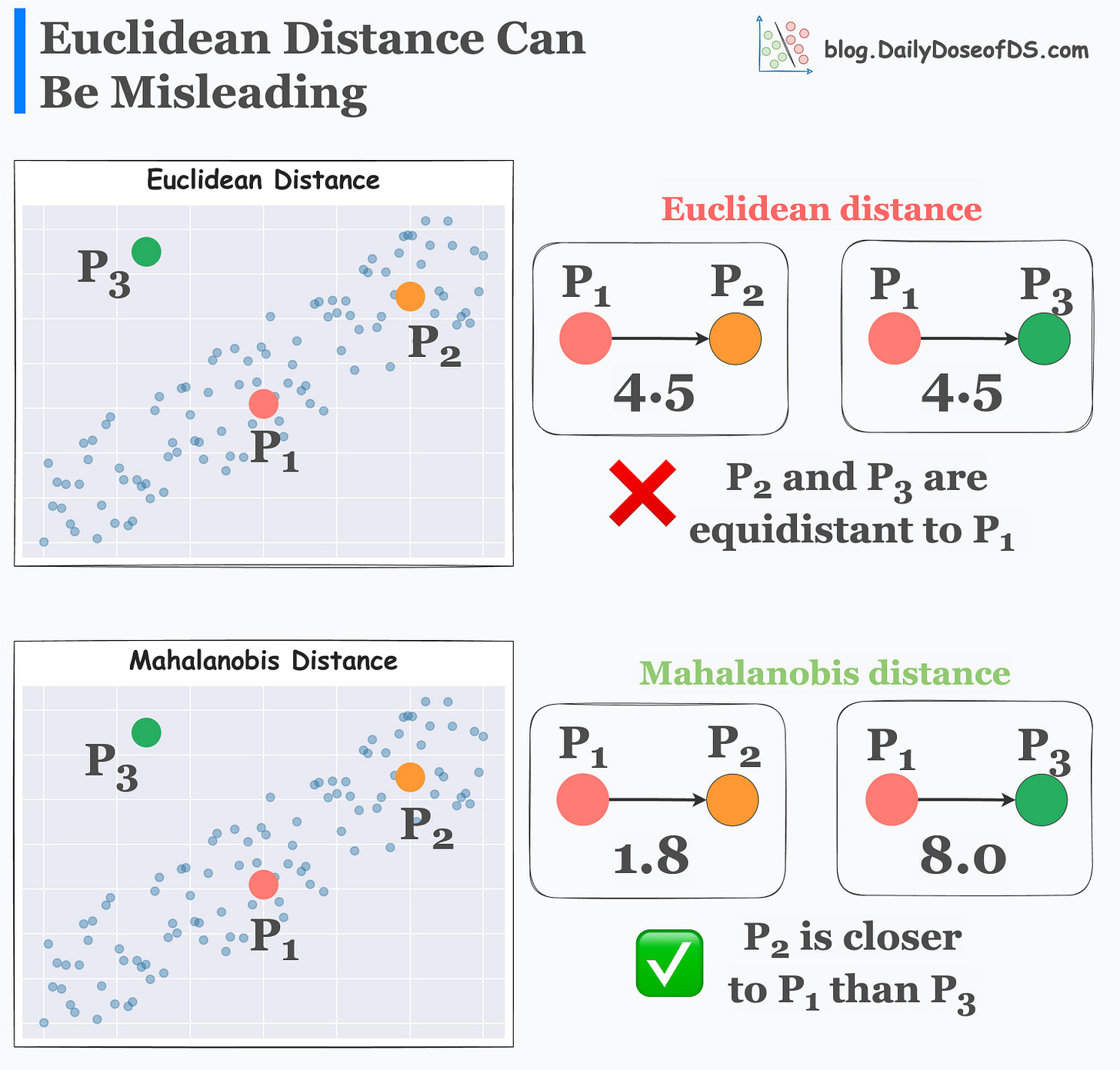
For instance, consider the scatter plot below:
Clearly, the features are correlated.
Consider three points — P1, P2, and P3.
There’s something that tells us that P2 is closer to P1 than P3. This is because P2 lies closer to the data distribution than P3.
Yet, Euclidean distance will still say that P2 and P3 are equidistant to P1.
Mahalanobis distance addresses this limitation.
It is a distance metric that takes into account the data distribution.
As a result, it can measure how far away a data point is from the distribution, which Euclidean can not.
Its effectiveness over Euclidean distance is evident from the image below. Given a dataset:
Euclidean distance says that P2 and P3 are equidistant to P1.
Mahalanobis distance says that P2 is closer to P1 than P3.
In this case, Mahalanobis distance is better because P2 is indeed closer to the data distribution.
How does it work?
The core idea behind Mahalanobis distance is similar to what we do in Principal Component Analysis (PCA).
We also discussed in detail in one of the recent deep-dives on PCA: Formulating the Principal Component Analysis (PCA) Algorithm From Scratch.
In a gist, the objective is to construct a new coordinate system with independent and orthogonal axes.
Computationally, it works as follows:
Step 1: Transform the columns into uncorrelated variables.
Step 2: Scale the new variables to make their variance equal to 1.
Step 3: Find the Euclidean distance in this new coordinate system.
So, eventually, we do use Euclidean distance.
However, we first transform the data to ensure that it obeys the assumptions of Euclidean distance.
If you wish to learn this in more detail, feel free to check the in-depth article on PCA: Formulating the Principal Component Analysis (PCA) Algorithm From Scratch.
👉 Over to you: What are some other limitations of Euclidean distance?
👉 If you liked this post, don’t forget to leave a like ❤️. It helps more people discover this newsletter on Substack and tells me that you appreciate reading these daily insights. The button is located towards the bottom of this email.
Thanks for reading!
Whenever you’re ready, here are a couple of more ways I can help you:
Get the full experience of the Daily Dose of Data Science. Every week, receive two deep dives that:
Make you fundamentally strong at data science and statistics.
Help you approach data science problems with intuition.
Teach you concepts that are highly overlooked or misinterpreted.
Promote to 32,000 subscribers by sponsoring this newsletter.
👉 Tell the world what makes this newsletter special for you by leaving a review here :)
👉 If you love reading this newsletter, feel free to share it with friends!






How do we use other clustering methods as KNN primarily uses Euclidean distances ?
FYI, I really look forward to receiving your daily updates! They are filled with usable nuggets of info. THANK YOU!