Where Did The Regularization Term Originate From?
An intuitive and probabilistic guide to regularization.
One of the major aspects of training any reliable ML model is avoiding overfitting.
In a gist, overfitting occurs when a model learns to perform exceptionally well on the training data.
This may happen because the model is trying too hard to capture all unrelated and random noise in our training dataset, as shown below:
And one of the most common techniques to avoid overfitting is regularization.
Simply put, the core objective of regularization is to penalize the model for its complexity.
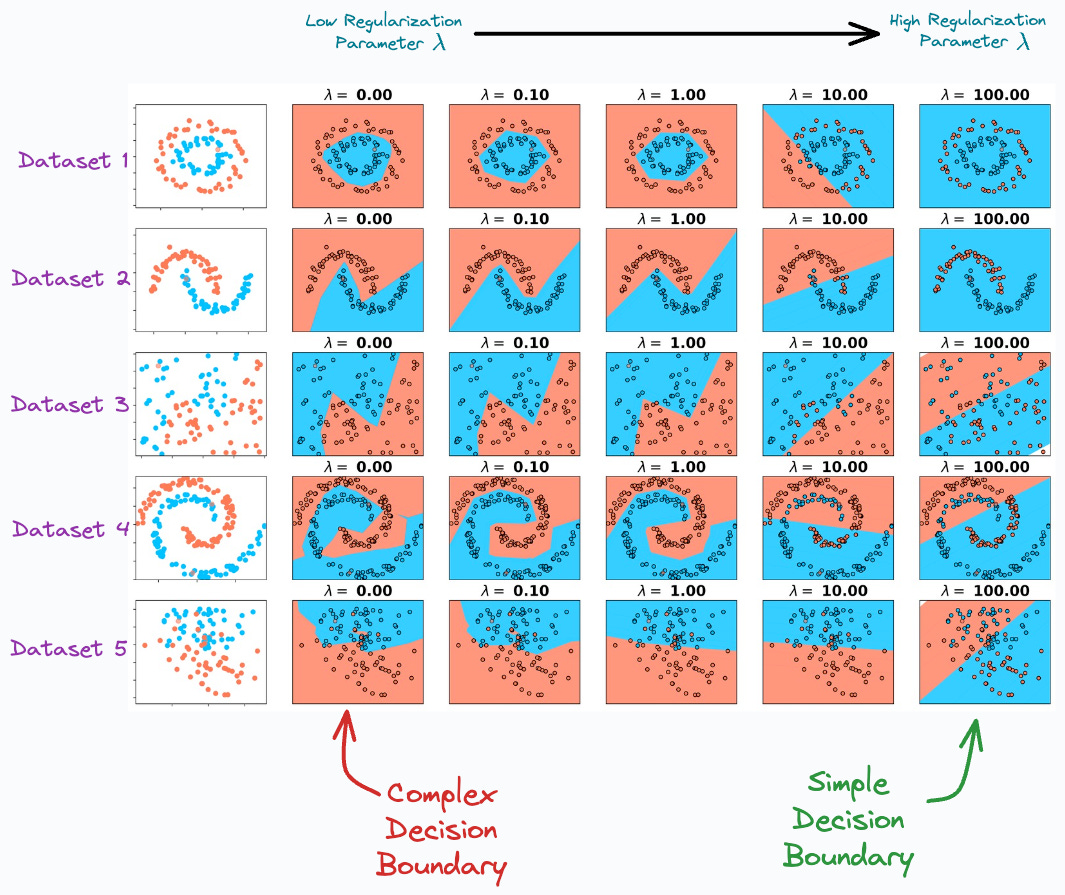
In fact, we can indeed validate the effectiveness of regularization experimentally, as shown below:
As we move to the right, the regularization parameter increases. As a result, the model creates a simpler decision boundary on all 5 datasets.
Now, if you have taken any ML course or read any tutorials about this, the most common they teach is to add a penalty (or regularization) term to the cost function, as shown below:
But why?
In other words, have you ever wondered why we are taught to add a squared term to the loss function (when using L2 regularization)?
In my experience, most tutorials never bother to cover it, and readers are always expected to embrace these notions as a given.
Yet, there are many questions to ask here:
Where did this regularization term originate from? How was it derived for the first time?
What does the regularization term precisely measure?
Why do we add this regularization term to the loss?
Why do we square the parameters (specific to L2 regularization)? Why not any other power?
Is there any probabilistic evidence that justifies the effectiveness of regularization?
Turns out, there is a concrete probabilistic justification for using regularization.
And if you are curious, then this is precisely the topic of today’s machine learning deep dive: “The Probabilistic Origin of Regularization.”
While most of the community appreciates the importance of regularization, in my experience, very few learn about its origin and the mathematical formulation behind it.
It can’t just appear out of nowhere, can it?
Thus, the objective of this deep dive is to help you build a solid intuitive, and logical understanding of regularisation — purely from a probabilistic perspective.

👉 Interested folks can read it here: The Probabilistic Origin of Regularization.
Hope you will learn something new today :)
👉 If you liked this post, don’t forget to leave a like ❤️. It helps more people discover this newsletter on Substack and tells me that you appreciate reading these daily insights. The button is located towards the bottom of this email.
Thanks for reading :)