Where Did the Regularization Term Originate From?
An intuitive and probabilistic guide to regularization.
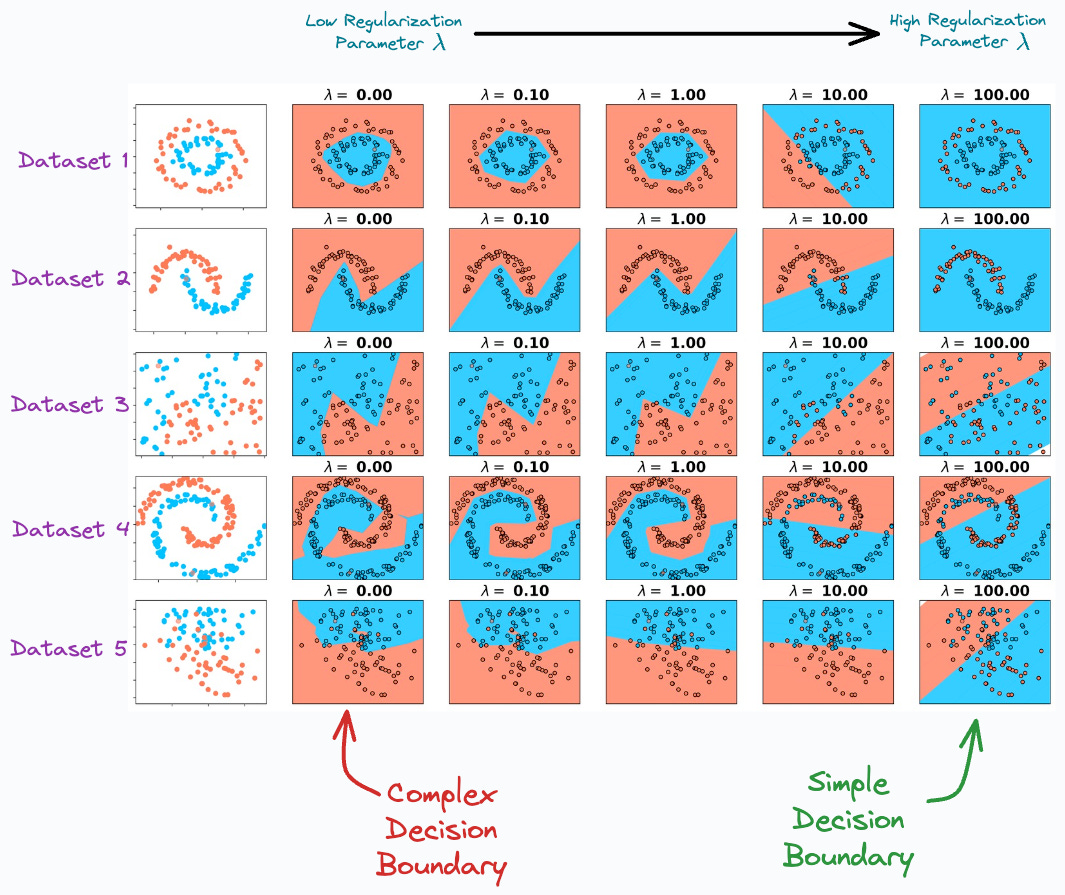
Experimentally, it’s pretty easy to verify the effectiveness of L2 Regularization, as shown below:
In the above plot, as we move to the right, the regularization parameter increases, and the model creates a simpler decision boundary on all 5 datasets.
The way we do this (which you likely already know) is by adding a penalty term to the loss function:
But why specifically a squared term?
Why not any other term when there are SO MANY functions we could have possibly used?
It turns out that there is a concrete probabilistic justification for using regularization.
If you are curious, we covered this in a beginner-friendly fashion here with a mathematical proof: The Probabilistic Origin of Regularization.
But here’s the gist.
Overfitting happens because the model attempts to capture all unrelated and random noise in our training dataset, as shown below:
And the core objective of regularization is to penalize the model for this complexity.
Regularization involves a slight modification to the maximum likelihood estimation (MLE) procedure, resulting in maximum a posteriori estimation (MAP).
MLE always attempts to find the parameters that are most likely to generate the data:
MAP also considers an initial belief about the parameters themselves:
As a result, the solution provided by MAP is typically more acceptable.
If it isn’t clear, let me give you an intuitive explanation of this.
An intuitive explanation
You are finding the weather extremely hot this year and intolerable compared to previous years.
You want to figure out the reason so you come up with the following three possibilities:
Personal sensitivity to heat.
The earth has moved closer to the sun relative to how far it was last year.
Climate change, wildfires in nearby states, etc.
If you think about it, explanation #2 is guaranteed to result in extremely hot weather, right?
So, following a maximum likelihood estimation (MLE) approach would result in explanation #2 being the most likely reason.
In other words, in MLE, you just accept the explanation that will most likely generate the observation (or data); that’s it.
But there’s something that tells you that explanation #2 is not a perfect fit, right?
This is because such cosmic events happen over lakhs/millions of years.
Thus, the explanation itself (the earth moving closer to the sun) is highly unlikely to occur in the first place.
You took a maximum a posteriori estimation (MAP) by doing this.
Simply put, in addition to the most likely explanation, MAP also considers an initial belief about the explanation itself.
The “explanation,” in the machine learning modeling case, is the parameters.
A similar idea is utilized in regularization:
Don’t just look at which parameters most likely generated the data, but also consider how likely the parameters are to appear themselves.
If you have taken any ML course or read tutorials about this, they most commonly teach to add a penalty (or regularization) term to the cost function.
However, they never bother to cover the origin story, and readers are always expected to embrace these notions as a given.
Yet, there are many questions to ask here:
Where did this regularization term originate from? How was it derived for the first time?
What does the regularization term precisely measure?
Why do we add this regularization term to the loss?
Why do we square the parameters (specific to L2 regularization)? Why not any other power?
Is there any probabilistic evidence that justifies the effectiveness of regularization?
It turns out that there is a concrete probabilistic justification for using regularization.
If you want to learn more, I covered its entire mathematical foundation in a beginner-friendly manner here: The Probabilistic Origin of Regularization.
Are you overwhelmed with the amount of information in ML/DS?
Every week, I publish no-fluff deep dives on topics that truly matter to your skills for ML/DS roles.
For instance:
A Beginner-friendly Introduction to Kolmogorov Arnold Networks (KANs)
5 Must-Know Ways to Test ML Models in Production (Implementation Included)
Understanding LoRA-derived Techniques for Optimal LLM Fine-tuning
8 Fatal (Yet Non-obvious) Pitfalls and Cautionary Measures in Data Science
Implementing Parallelized CUDA Programs From Scratch Using CUDA Programming
You Are Probably Building Inconsistent Classification Models Without Even Realizing
And many many more.
Join below to unlock all full articles:
SPONSOR US
Get your product in front of 82,000 data scientists and other tech professionals.
Our newsletter puts your products and services directly in front of an audience that matters — thousands of leaders, senior data scientists, machine learning engineers, data analysts, etc., who have influence over significant tech decisions and big purchases.
To ensure your product reaches this influential audience, reserve your space here or reply to this email to ensure your product reaches this influential audience.