In yesterday’s post, we learned why Sklearn’s linear regression class has no hyperparameter.
More specifically, we saw it implements the ordinary least squares (OLS) method, and the coefficient estimates are:
where,
X: input features with dimensions(n,m).y: response variable with dimensions(n,1).Θ: estimates with dimensions(m,1).n: number of samples.m: number of features.
Now, in the data science and statistics community, the OLS estimator is known as an unbiased estimator.
What do we mean by that?
Why is OLS called such?
Let’s understand this today!
Background
The goal of statistical modeling is to make conclusions about the whole population.
However, it is pretty obvious that observing the entire population is impractical.
In other words, given that we cannot observe (or collect data of) the entire population, we cannot obtain the true parameter (β) for the population:
Thus, we must obtain parameter estimates (B̂) on samples and infer the true parameter (β) for the population from those estimates:
And, of course, we want these sample estimates (B̂) to be reliable to determine the actual parameter (β).
The OLS estimator ensures that.
Let’s understand how!
True population model
When using a linear regression model, we assume that the response variable (Y) and features (X) for the entire population are related as follows:
β is the true parameter that we are not aware of.
ε is the error term.
Expected Value of OLS Estimates
As we saw yesterday, the closed-form solution of OLS is given by:
What’s more, as discussed above, using OLS on different samples will result in different parameter estimates:
Let’s find the expected value of OLS estimates E[B̂].
Simply put, the expected value is the average value of the parameters if we run OLS on many samples.
This is given by:
Here, substitute Y = βX + ε:
If you are wondering how we can substitute Y = βX + ε when we don’t know what β is, then here’s the explanation:
See, we can do that substitution because even if we don’t know the parameter β for the whole population, we know that the sample was drawn from the population.
Thus, the equation in terms of the true parameters (Y = βX + ε) still holds for the sample.
Let me give you an example.
Say the population data was defined by y = sin(x) + ε. Of course, we wouldn’t know this, but just keep that aside for a second.
Now, even if we were to draw samples from this population data, the true equation y = sin(x) + ε would still be valid on the sampled data points, wouldn’t it?
The same idea has been extended for expected value.
Coming back to the following:
Let’s open the inner parenthesis:
Simplifying, we get:
And finally, what do we get?
The expected value of parameter estimates on the samples equals the true parameter value β.
And this is precisely what the definition of an unbiased estimator is.
More formally, an estimator is called unbiased if the expected value of the parameters is equal to the actual parameter value.
And that is why we call OLS an unbiased estimator.
An important takeaway
Many people misinterpret unbiasedness with the idea that the parameter estimates from a single run of OLS on a sample are equal to the true parameter values.
Don’t make that mistake.
Instead, unbiasedness implies that if we were to generate OLS estimates on many different samples (drawn from the same population), then the expected value of obtained estimates will be equal to the true population parameter.
And, of course, all this is based on the assumption that we have good representative samples and that the assumptions of linear regression are not violated.
What are these assumptions? Learn them here.
👉 Over to you: What are some other properties of the OLS estimator?
👉 If you liked this post, don’t forget to leave a like ❤️. It helps more people discover this newsletter on Substack and tells me that you appreciate reading these daily insights.
The button is located towards the bottom of this email.
Thanks for reading!
Latest full articles
If you’re not a full subscriber, here’s what you missed:
DBSCAN++: The Faster and Scalable Alternative to DBSCAN Clustering
Federated Learning: A Critical Step Towards Privacy-Preserving Machine Learning
You Cannot Build Large Data Projects Until You Learn Data Version Control!
Sklearn Models are Not Deployment Friendly! Supercharge Them With Tensor Computations.
Deploy, Version Control, and Manage ML Models Right From Your Jupyter Notebook with Modelbit
Gaussian Mixture Models (GMMs): The Flexible Twin of KMeans.
To receive all full articles and support the Daily Dose of Data Science, consider subscribing:
👉 Tell the world what makes this newsletter special for you by leaving a review here :)
👉 If you love reading this newsletter, feel free to share it with friends!














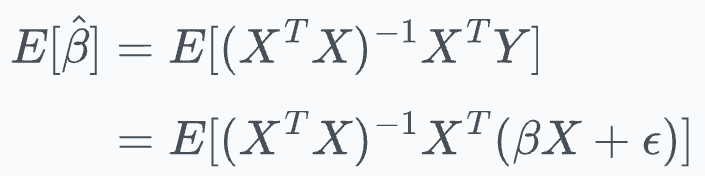





Vector form of Y should be Y=X beta + epsilon. What you have the dimension doesn’t add up.
Very important concepts that touch on statistic's fundamentals. Really love these "low-level" topics!