Why Mean Squared Error (MSE)?
Why not any other loss function?
Say you wish to train a linear regression model. We know that we train it by minimizing the squared error:
But have you ever wondered why we specifically use the squared error?
See, many functions can potentially minimize the difference between observed and predicted values. But of all the possible choices, what is so special about the squared error?
In my experience, people often say:
Squared error is differentiable. That is why we use it as a loss function. WRONG.
It is better than using absolute error as squared error penalizes large errors more. WRONG.
Sadly, each of these explanations are incorrect.
But approaching it from a probabilistic perspective helps us understand why the squared error is the ideal choice.
Let’s begin.
In linear regression, we predict our target variable y using the inputs X as follows:
Here, epsilon is an error term that captures the random noise for a specific data point (i).
We assume the noise is drawn from a Gaussian distribution with zero mean based on the central limit theorem:
Thus, the probability of observing the error term can be written as:
Substituting the error term from the linear regression equation, we get:
For a specific set of parameters θ, the above tells us the probability of observing a data point (i).
Next, we can define the likelihood function as follows:
The likelihood is a function of θ. It means that by varying θ, we can fit a distribution to the observed data and quantify the likelihood of observing it.
We further write it as a product for individual data points because we assume all observations are independent.
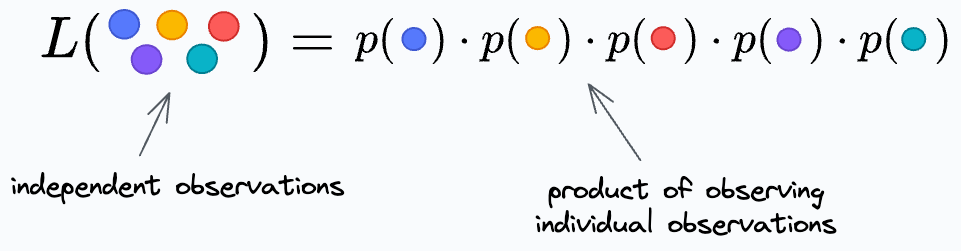
Thus, we get:
Since the log function is monotonic, we use the log-likelihood and maximize it. This is called maximum likelihood estimation (MLE).
Simplifying, we get:
To reiterate, the objective is to find the θ that maximizes the above expression.
But the first term is independent of θ. Thus, maximizing the above expression is equivalent to minimizing the second term.
And if you notice closely, it’s precisely the squared error.
Thus, you can maximize the log-likelihood by minimizing the squared error.
And this is the origin of least-squares in linear regression.
See, there’s clear proof and reasoning behind using squared error as a loss function in linear regression.
Nothing comes from thin air in machine learning :)
But did you notice that in this derivation, we made a lot of assumptions?
Firstly, we assumed the noise was drawn from a Gaussian distribution. But why?
We assumed independence of observations. Why and what if it does not hold true?
Next, we assumed that each error term is drawn from a distribution with the same variance σ. But what if it looks like this:
In that case, the squared error will come out to be:
How to handle this?
I discussed the origin of all assumptions of linear regression in detail here: Where Did The Assumptions of Linear Regression Originate From?
Thanks for reading!
Whenever you are ready, here’s one more way I can help you:
Every week, I publish 1-2 in-depth deep dives (typically 20+ mins long). Here are some of the latest ones that you will surely like:
[FREE] A Beginner-friendly and Comprehensive Deep Dive on Vector Databases.
A Detailed and Beginner-Friendly Introduction to PyTorch Lightning: The Supercharged PyTorch
You Are Probably Building Inconsistent Classification Models Without Even Realizing
Why Sklearn’s Logistic Regression Has no Learning Rate Hyperparameter?
PyTorch Models Are Not Deployment-Friendly! Supercharge Them With TorchScript.
Federated Learning: A Critical Step Towards Privacy-Preserving Machine Learning.
You Cannot Build Large Data Projects Until You Learn Data Version Control!
To receive all full articles and support the Daily Dose of Data Science, consider subscribing:
👉 If you love reading this newsletter, feel free to share it with friends!
👉 Tell the world what makes this newsletter special for you by leaving a review here :)









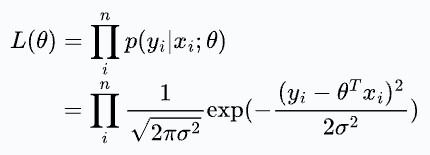
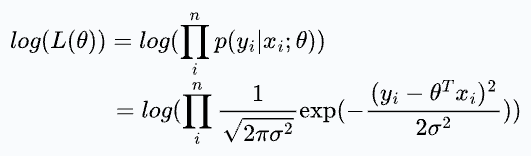




I love the low-level derivations; they always hit different and give you a unique understanding that many people gloss over. Keep this content coming!
Loved the post, can you though explain it in a more intuitive and less technical way, I am sure many people will appreciate it!