Your Random Forest Model is Never the Best Random Forest Model You Can Build

The coolest trick to improve random forest models.

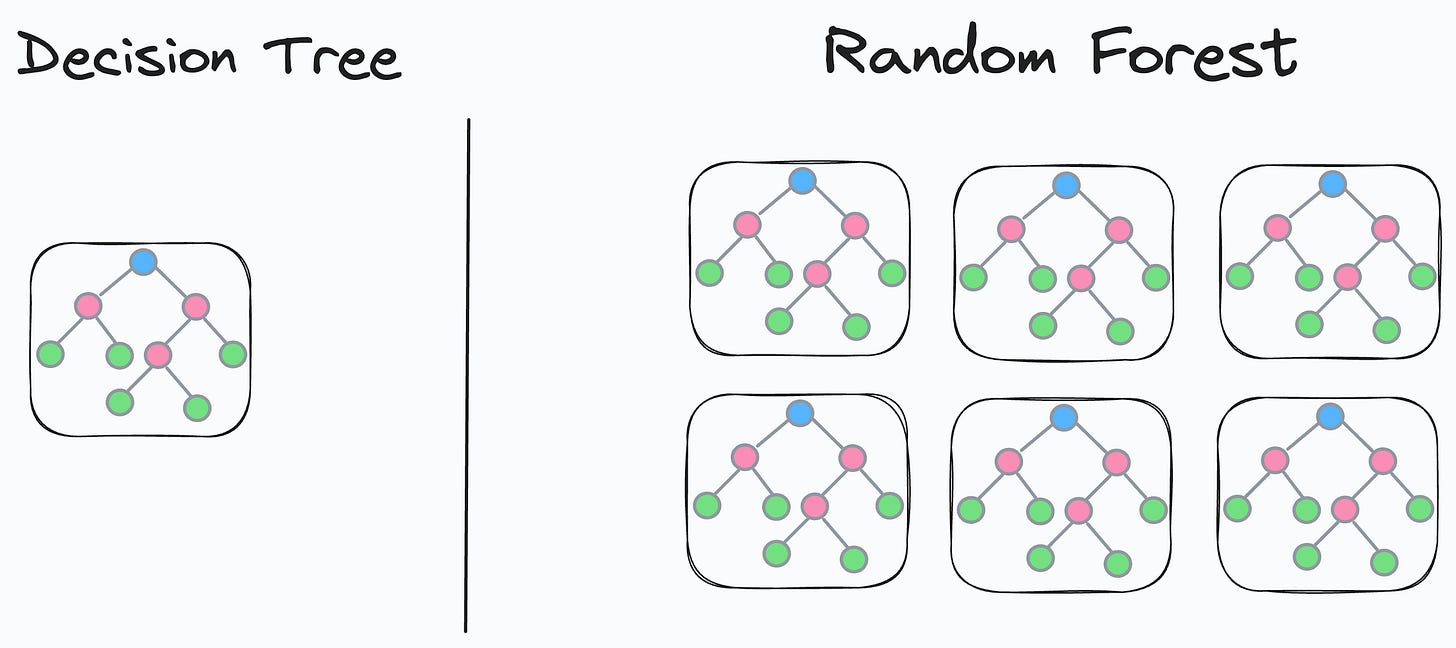
Random forest is a pretty powerful and robust model, which is a combination of many different decision trees.

But the biggest problem is that whenever we use random forest, we always create much more base decision trees than required.

Of course, this can be tuned as a hyperparameter, but it requires training many different random forest models, which takes time.

Today, I will share one of the most incredible tricks I formulated recently to:

• Increase the accuracy of a random forest model

• Decrease its size.

• Drastically increase its prediction run-time.

And all this without having to ever retrain the model.

Are you ready?

Let’s begin!

Logic

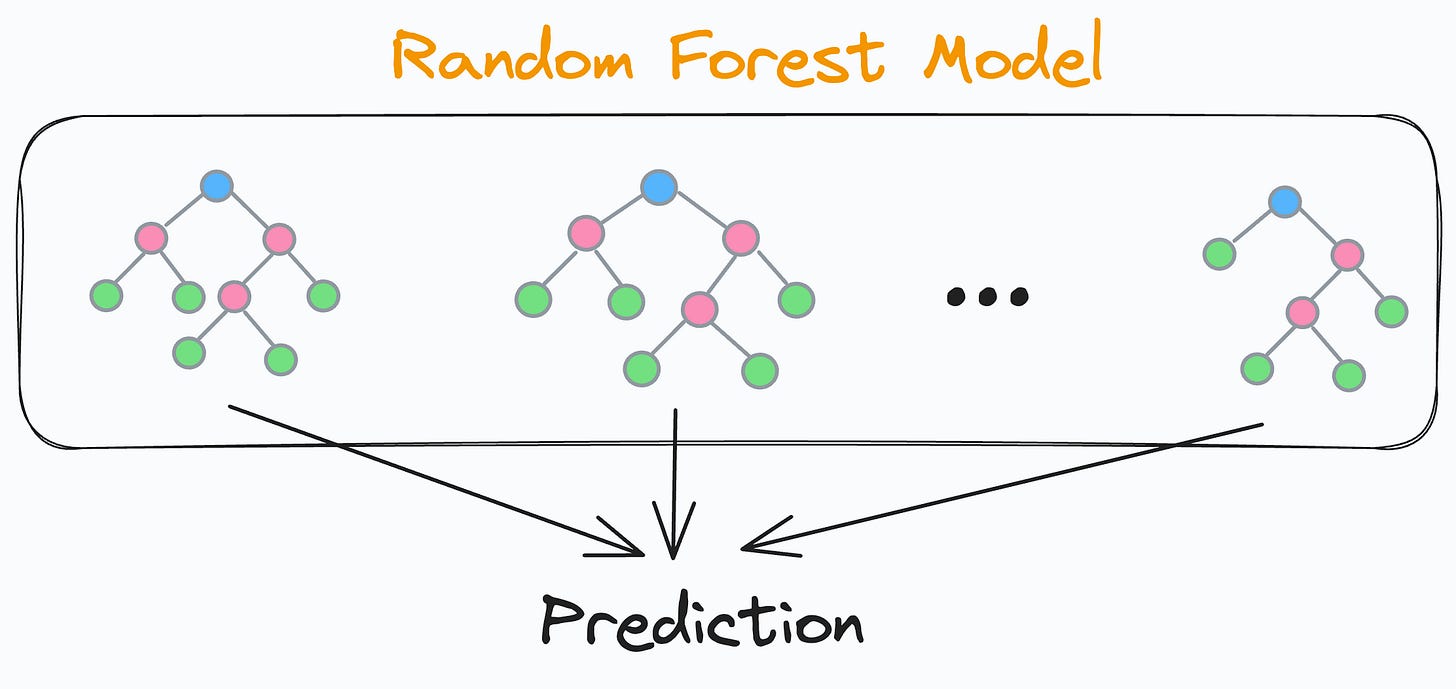
We know that a random forest model is an ensemble of many different decision trees:

The final prediction is generated by aggregating the predictions from each individual and independent decision tree.

As each decision tree in a random forest is independent, this means that each decision tree will have some test accuracy, right?

This also means that there will be some underperforming and some well-performing decision trees. Agreed?

So what if we do the following:

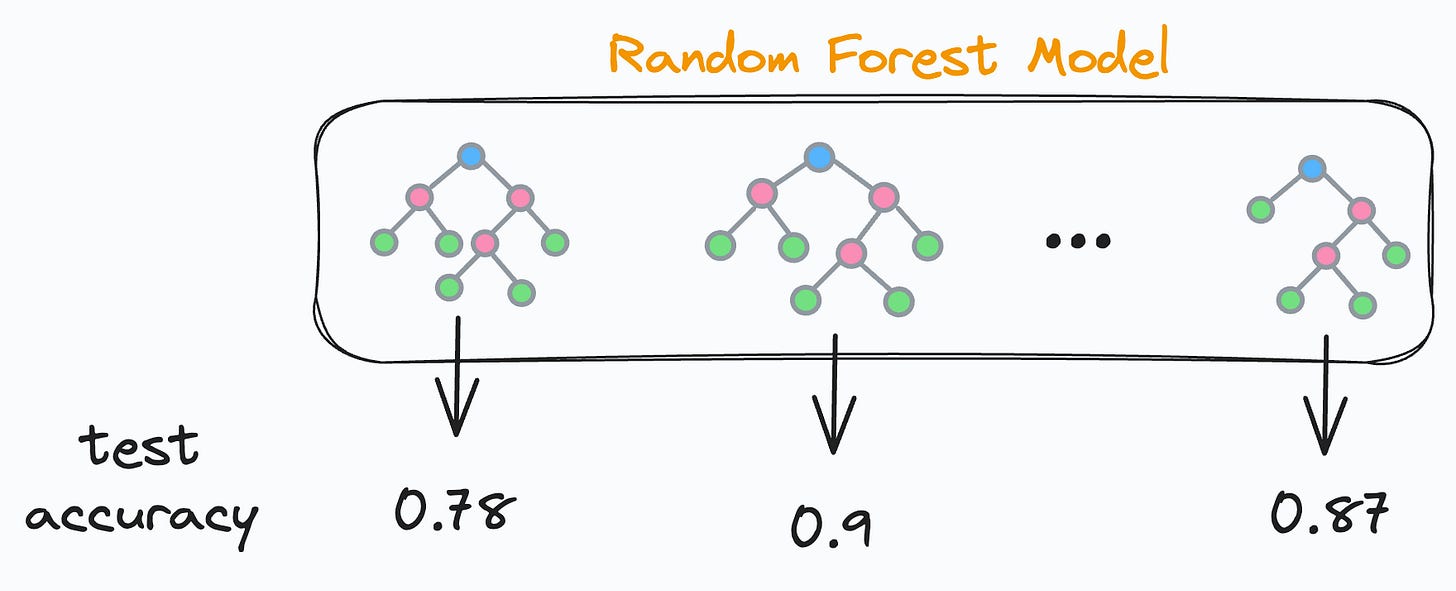
• We find the test accuracy of every decision tree.

• We sort the accuracies in decreasing order.

• We keep only the “k” top-performing decision trees and remove the rest.

Once done, we’ll be only left with the best-performing decision trees in our random forest, as evaluated on the test set.

Cool, isn’t it?

Now, how to decide “k”?

It’s simple.

We can create a cumulative accuracy plot.

It will be a line plot depicting the accuracy of the random forest:

• Considering only the first two decision trees.

• Considering only the first three decision trees.

• Considering only the first four decision trees.

• And so on.

It is expected that the accuracy will first increase with the number of decision trees and then decrease.

Looking at this plot, we can find the most optimal “k”.

Implementation

Let’s look at its implementation.

First, we train our random forest as we usually would:

Train the random forest model

Next, we must compute the accuracy of each decision tree model.

In sklearn, individual trees can be accessed with model.estimators_ attribute.

Estimators of random forest are a list of decision trees

Thus, we iterate over all trees and compute their test accuracy:

Compute the accuracy of all trees

The model_accs is a NumPy array that stores tree id and its test accuracy:

>>> model_accs
array([[ 0.   ,  0.815], # [tree id, test accuracy]
       [ 1.   ,  0.77 ],
       [ 2.   ,  0.795],
          ...

Now, we must rearrange the decision tree models in the model.estimators_ list in decreasing order of test accuracies:

# sort on second column in reverse order to obtain sorting order
>>> sorted_indices = np.argsort(model_accs[:, 1])[::-1]

# obtain list of model ids according to sorted model accuracies
>>> model_ids = model_accs[sorted_indices][:,0].astype(int)
array([65, 97, 18, 24, 38, 11,...

This list tells us that the 65th indexed model is the highest performing, followed by 97th indexed, and so on….

Now, let’s rearrange the tree models in model.estimators_ list in the order of model_ids:

# create numpy array, rearrange the models and convert back to list
model.estimators_ = np.array(model.estimators_)[model_ids].tolist()

Done!

Finally, we create the plot discussed earlier.

It will be a line plot depicting the accuracy of the random forest:

• By considering only the first two decision trees.

• By considering only the first three decision trees.

• By considering only the first four decision trees.

• and so on.

The code to compute cumulative accuracies is demonstrated below:

Create the cumulative accuracy plot

In the above code:

• We create a copy of the base model called small_model.

• In each iteration, we set small_model’s trees to the first “k” trees of the base model.

• Finally, we score the small_model with just “k” trees.

Plotting the cumulative accuracy result, we get the following plot:

Cumulative accuracy score

It is clear that the max test accuracy appears by only considering 10 trees, which is a ten-fold reduction in the number of trees.

Comparing their accuracy and run-time, we get:

• We get a 3% accuracy boost.

• 6.5 times prediction faster run-time.

Now, tell me something:

• Did we do any retraining or hyperparameter tuning? No.

• As we reduced the number of decision trees, didn’t we improve the run time? Of course, we did.

Isn’t that cool?

Of course, we may not want to overly reduce the ensemble size because we want to ensure our RF still maintains many different types of decision trees.

Thus, the approach to selecting the best k can be quite subjective and it does not necessarily have to rely solely on the validation accuracy but could be based on various factors.

What are your thoughts?

You can download this notebook here: Jupyter Notebook.

👉 Over to you: What are some other cool ways to improve model run-time?

👉 If you liked this post, don’t forget to leave a like ❤️. It helps more people discover this newsletter on Substack and tells me that you appreciate reading these daily insights. The button is located towards the bottom of this email.

Thanks for reading!

---

Latest full articles

If you’re not a full subscriber, here’s what you missed last month:

• Sklearn Models are Not Deployment Friendly! Supercharge Them With Tensor Computations.

• Deploy, Version Control, and Manage ML Models Right From Your Jupyter Notebook with Modelbit

• Model Compression: A Critical Step Towards Efficient Machine Learning.

• Generalized Linear Models (GLMs): The Supercharged Linear Regression.

• Gaussian Mixture Models (GMMs): The Flexible Twin of KMeans.

• Bayesian Optimization for Hyperparameter Tuning.

• Formulating the PCA Algorithm From Scratch.

To receive all full articles and support the Daily Dose of Data Science, consider subscribing:

---

👉 Tell the world what makes this newsletter special for you by leaving a review here :)

👉 If you love reading this newsletter, feel free to share it with friends!